Ультравысокие давления в геологии (гораздо большие, чем те, с которыми мы можем столкнуться, изучая литосферу Земли) появляются в двух главных случаях: если мы спускаемся ниже литосферы, в глубины мантии Земли (или землеподобных планет), либо при падениях метеоритов.
Приготовление молотого кофе в ступке Абиха из зернового методом ударных нагрузок.
Между этими двумя давлениями есть принципиальная разница, заключающаяся в скорости его появления и исчезновения. Падение метеорита - это мгновенный удар, когда давление появляется и исчезает за секунды (не считая времени релаксации системы), а литостатические давления сохраняются миллиарды лет.
В предыдущем посте я писал про уравнения состояния вещества в условиях сверхвысоких давлений. Этот пост будет посвящён экспериментальным методам изучения воздействия сверхвысоких давлений на вещество и методам получения констант для этих уравнений.
Методы изучения экстремальных состояний вещества идут из военного дела и аэро- и космонавтики. Поведение вещества мишени при попадании в него снаряда-ударника или даже в условиях ядерного взрыва весьма отлично от поведения в "обычных" условиях. Особенности великолепно видно в сверхскоростных съёмках типа этого видео (весьма рекомендую):
Видео (c) Werner Mehl, 2009
Задачи этого изучения (из тех, которые сразу приходят в голову):
- Материаловедение, поиск устойчивых к шоковым нагрузкам веществ (техногенные катастрофы, военные действиях, космонативка).
- Материаловедение, поиск веществ с заданными свойствами. Например, технические алмазы в качестве абразивного материала.
- Чисто фундаментальные (не дающие "бонусов" в ближайшем будущем) задачи геологии (вымирание динозавров) и планетологии (особенно формирования планет). Глубинная геофизика и астрономия (поиск землеподобных экзопланет).
- Задачи рудной и безрудной геологий. Например, месторождение медно-никелевых руд Садбери, одно из крупнейших в мире, было сформировано именно благодаря плавлению больших объёмов вещества из-за удара материала. Или крупнейшее в мире месторождение алмазов - Попигайская астроблема.
- И, "ви будете смеяться", но решение некоторых вопросов археологии. Помимо знаменитых мечей и прочих предметов из метеоритного железа, импактные породы использовались
по назначениюдля обкладки костров древними людьми. Позднее тектиты (импактные стёкла) использовались для изготовления украшений.
Методы изучения.
Экстраполировать свойства веществ при нормальных температурах и давлениях на ударные и экстремальные нагрузки, конечно, неверно. Первый же фазовый переход (хоть то же плавление) поставит на этом большой и жирный крест.
Компьютерное моделирование работает, но только в определённых пределах. Про некоторые достижения и проблемы я писал в прошлом посте.
Остаётся только путь экспериментов.
Для экспериментов в условиях высоких постоянных давлений есть два главных варианта. Это многопуансонные аппараты (Multianvil presses), которые работают лишь до ~25 ГПа, и алмазные наковальни (diamond anvil cells), которые позволяют достичь давлений в 300 ГПа (для сравнения, на границе ядра и мантии Земли 136 ГПа).
В алмазных наковальнях вещество помещается между двумя алмазами, которые его сдавливают. "Коническая" форма алмазов позволяет, приложив маленькое давление к экспериментальной ячейке, получить большое давление в образце. Большим плюсом является то, что прозрачные алмазы позволяют непосредственно наблюдать и изучать (рентген и другие виды проникающего излучения) вещество в процессе опыта.
Картинка из Википедии: Diamond Anvil Cell - Cross Section" by Tobias1984
Проблема состоит в том, что мы можем оценить давление (с точностью порядка 5%), температуру (с примерно такой же точностью), и можем понять, что там находится (узнать параметры кристаллической решётки с помощью рентгена). На этом, в общем, все измеряемые свойства вещества заканчиваются. Хотя, надо отметить, сейчас появляются методики изучения вещества в алмазных наковальнях с помощью упругих волн (напр. [Jacobsen et al., 2005]), но это всё ещё не рутинные методы, и, опять же, это далеко не все свойства.
Хорошая статья, описывающая данный метод в применении к геологии - "High-pressure experiments and the phase diagram of lower mantle and core materials" [Boehler, 2009]".
В том случае, если нам нужны какие-то физические свойства этого вещества, этот нам не подходит.
Если нам надо узнать свойства вещества при ударных нагрузках, на помощь приходят эксперименты с ударной волной (shock wave experiments). Довольно простая обзорная статья с хорошими картинками лежит тут.
Одна из схем установок - это эксперименты со сферической ударной волной.
Рисунок по Gubbins & Herrero-Bervera "Encyclopedia of Geomagnetism and Paleomagnetism". Взрыв приводит к мгновенному разгону flyer plate до скоростей 9-11 км/с, которая ударяется в driver plate, которая уже равномерно перераспределяет давление на образец.
В геологии этот метод применяется, в частности, для изучения преобразования вещества при ударе метеоритов. Здесь я копирую слайд из лекций по курсу "Петрология метеоритов и импактитов" В.И. Фельдмана (2009 г.)
"После взрыва ударная волна, двигаясь к центру, создаёт на поверхности шара нагрузку около 25 ГПа, а в 1 мм от центра до 350 ГПа. (...) время сжатия образца составляет 1 – 3 миллионных доли секунды, температура в центре шара достигает 12 тыс градусов, а охлаждение начинается со скоростью сотен миллионов градусов в секунду. Поэтому в образце сохраняются высокотемпературные и высокоплотные полиморфные модификации минералов, не происходит отжига или автогидротермальных изменений, характерных для астроблем, где запасы тепла многократно больше, а скорости осывания на порядки меньше. На фото зональность в образце гранита после сферического нагружения." (c) В.И. Фельдман
Этот метод позволяет изучать фазовые переходы в веществе при ударных нагрузках и вынужденную химическую диффузию (под действием ударной волны), но термодинамика и ударные свойства вещества остаются и тут неизвестны (с той точностью, которая необходима для моделирования их поведения).
Наконец, тот метод, который получил сейчас наибольшее распространение, поскольку современные технологии позволяют "вытащить" из него реологические и термодинамические свойства вещества - это метод нагружения плоской ударной волной. Есть два главных варианта создания нагрузки - газовой пушкой или лазером.
В газовой пушке (Light gas gun) происходит взрыв, разгоняющий первый ударник. Он движется в газовой среде (водородной или гелиевой), создавая резкое её сжатие. Газ с низкой молекулярной массой способен расширяться быстрее, чем пороховые газы с более высокой массой:
\[c = \sqrt{\frac{KV}{M}}\]
где $c$ - скорость звука, $K$ - модуль объёмного сжатия, $V$ - удельный объём моля вещества, $M$ - молярная масса. Чем больше молярная масса, тем меньше скорость и ниже получаемое в мишени давление. Соответственно, использование лёгкого газа позволяет достичь более высоких скоростей ударника при попадании в мишень.
В газовой пушке (Light gas gun) происходит взрыв, разгоняющий первый ударник. Он движется в газовой среде (водородной или гелиевой), создавая резкое её сжатие. Газ с низкой молекулярной массой способен расширяться быстрее, чем пороховые газы с более высокой массой:
\[c = \sqrt{\frac{KV}{M}}\]
где $c$ - скорость звука, $K$ - модуль объёмного сжатия, $V$ - удельный объём моля вещества, $M$ - молярная масса. Чем больше молярная масса, тем меньше скорость и ниже получаемое в мишени давление. Соответственно, использование лёгкого газа позволяет достичь более высоких скоростей ударника при попадании в мишень.
Компания QuickLaunch медленно и печально пытается наладить отправку спутников в космос с помощью подобной пушки. Если получится, это будет очень дешёвым методом.Другой метод - это лазерная пушка:
Лазерное излучение, пройдя через прозрачное "окошко", испаряет в плазму рабочее вещество, давление расширяющейся плазмы толкает ударник (flyer), и он бьёт в мишень (sample). Опять же, часто используется driver plate для передачи давления. Схема из "Laser-induced shock waves in condensed matter: some techniques and applications" [Luo et al., 2004].
Принципиальным преимуществом метода плоской ударной волны является возможность измерения множества параметров. Базовым является скорость перемещения ударника (flyer) и ударной волны, которая обычно измеряется методом лазерной интерферометрии VISAR. Созданное давление рассчитывается, исходя из знания свойств плазмы при приложении определённого количества энергии (при нагреве лазером). Определение температуры является одной из наиболее сложных процедур в этих экспериментах.
В настоящее время существуют возможности определения фазового и структурного состава вещества в момент прохождения волны. Более того, есть возможности получения развёртки во времени некоторых параметров среды, включая кавитацию - формирование пустот внутри материала (см. напр. тут). Более подробная статья, посвящённая изменениям материалов в условиях ударных волн, есть тут (хотя, конечно, их очень и очень много).
В своём прошлом посте я постарался подробно рассказать об основных особенностях уравнения состояния вещества. В статье фигурировало довольно много параметров, измерение которых осталось за кадром. Сейчас же, после обращения к экспериментальным методам, можно сказать и о методиках измерения параметров.
Главное допущение. В момент прохождения ударной волны у нас есть два состояния вещества - до сжатия и после сжатия, между которыми проходит фронт волны, по многим свойствам аналогичный фазовой границе. Поэтому, исходя из уравнений сохранения импульса и энергии мы можем вывести несколько базовых формул.
Главная формула - это уравнение Ранкиля-Гюгонио (Rankine–Hugoniot):
\[\rho_H (U_s - u_p) = \rho_o U_s\]
которое связывает плотность вещества после сжатия $\rho_H$, до сжатия $\rho_0$ со скоростями ударной волны $U_s$ и скоростью частиц $u_p$. Скорость частиц - это скорость перемещений атомов вещества, непосредственное измерение которой представляет значительную сложность.
\[ u_p = u_{fp} + \frac{C_{0,fp} + U_s\frac{\rho_{0}}{\rho_{0,fp}}}{2S_{fp}} - \sqrt {\left(\frac{C_{0,fp} + U_s\frac{\rho_{0}}{\rho_{0,fp}}}{2S_{fp}}\right)^2 + \frac{ \frac{\rho_{0}}{\rho_{0,fp}} U_s u_{fp} }{S_{fp}} }\]
где $u_p$ - скорость частиц, $u_{fp}$ - скорость flyer plate, $U_s$ - скорость ударной волны, $\rho_{0,fp}$, $\rho_{0}$ - плотность flyer plate и вещества мишени в нормальных условиях, $S$ и $C_0$ связаны между собой уравнением:
\[ U_s = C_0 + Su_p \equiv \sqrt {\frac{K_{S,0}}{\rho_{0}}} + \frac{K_S' + 1}{4}u_p \]
где $K_{S,0}$ - изоэнтропный объёмный модуль сжатия, а $K_S' = \frac{dK_S}{dP}$ (подробнее в предыдущем посте).
Далее, мы можем из пространства скорости ударной волны и скорости частиц перейти к пространству давления-объёма, то есть термодинамических параметров:
\[ u_p = \sqrt{(P_1-P_0)(V_0-V_1)} \]
\[ U_s = V_0\sqrt{\frac{P_1-P_0}{V_0-V_1}} \]
Также можно перейти к внутренним энергиям (обозначаются E или U, здесь изложение по [Mosenfelder et al., 2007]). Есть базовая формула, связывающая разницу внутренних энергий вещества в шоковом состоянии (индекс $H$) и вещества на изоэнтропе (при адиабатическом сжатии, то есть, грубо говоря, без обмена теплом, индекс 0):
\[ \Delta E_H = \frac{P_H}{2} \left( \frac{1}{\rho_0}- \frac{1}{\rho_H} \right)\]
Изоэнтропа же определяется уравнением статического сжатия (т.е. уравнением, связывающим плотность только с давлением, без изменения температуры), например, то уравнение Birch-Murnaghan, о котором я говорил в прошлом посте. Для него изменение внутренней энергии переписывается в виде:
\[ \Delta E_S = \frac{9 K_{S,0}}{2\rho_0} \left( \frac{(\rho_H/\rho_0)^{2/3}-1}{2}\right)^2 \left( 1 + (K'_{S}-4) \left( \frac{(\rho_H/\rho_0)^{2/3}-1}{2}\right) \right)\]
Так как нам надо от изоэнтропы перейти к гюгониоте (так называется график ударного сжатия в P-V координатах), то надо к этой $\Delta E_S$ добавить энергию перехода (этот подход вместе с допущением о зависимости параметра Грюнайзена $\gamma$ только от давления) обобщается в теории Mie-Gruneisen):
\[ \Delta E_V = \frac{P_H - P_S}{\gamma \rho_H} = \frac{P_H - P_S}{\gamma_0 (\rho_H/\rho_0)^q \rho_H}\]
Теперь, если мы просуммируем эти энергии и добавим энергию возможных фазовых переходов $\Delta E_{tr}$ (что делается просто как разность энергий образования веществ), мы получим:
\[ \Delta E_H = \Delta E_S + \Delta E_V+ \Delta E_{tr} \]
Совокупность этих уравнений позволяет создать термодинамическую взаимосогласованную расчётную базу.
Термодинамические и реологические свойства веществ
Итак, в вышеприведённом тексте у нас фигурировали (помимо состояния вещества при заданных параметрах $\rho_0-P_0-T_0$) модуль объёмного сжатия $K_S$, его производная по давлению $K_S'$, параметр Грюнайзена $\gamma$ (внимание! это не отношение теплоёмкостей из теории газов!!), параметр Грюнайзена второго порядка $q$.
Модуль объёмного сжатия и его производная устанавливаются по вышеприведённым уравнениям.
Параметры Грюнайзена $\gamma$ и $q$ устанавливаются, если установить несколько гюгониот при постоянном объёме (но разной внутренней энергии, напр. [Mosenfelder, 2007b]).
Количество переменных для поиска нередко сужают, принимая некоторые параметры фиксированными (исходя из свойств подобных веществ или предыдущих исследований). В принципе, с учётом того, что возможных параметров для варьирования достаточно много, остаётся достаточно степеней свободы.
Зная эти параметры, можно рассчитать изотермический модуль сжатия $K_T$ и его производную по давлению $K_T'$ (при необходимости и начилии данных- и $dK_T/dT$), которые и нужны для уравнений состояния (см. прошлый пост).
Последний необходимый параметр, который нам нужен - это коэффициент термического расширения $\alpha$ или теплоёмкость $C_V$. Они абсолютно взаимозаменяемы при известных вышеперечисленных, как следует из формулы:
\[ C_V = \frac{\alpha K_T}{\gamma \rho} \]
Есть несколько подходов.
Непосредственная калориметрия в условиях сверхвысоких давлений и температур не реализуема. Во всяком случае, не видел я таких работ.
Простой и совсем плохой - это взять теплоёмкость при низких давлениях и использовать её.
Второй и немного получше - это использовать, в конечном счёте, теплоёмкость по Дебаю. В принципе, при известных скоростях звука в среде это получается довольно адекватный метод. Но только если они известны.
Третий метод, который уже основан на измерениях. Это измерение коэффициента температурного расширения. Это возможно проделать в качестве довольно рутинной процедуры в описанной выше установке с алмазными наковальнями. Метод дифракции рентгеновских лучей (X-ray diffraction) позволяет провести непосредственное измерение объёма элементарной ячейки кристаллической фазы in situ, т.е. в условиях эксперимента (напр. [Mao et al., 2011]).
PS: алмазные наковальни, теоретически, позволяют также калибровать уравнения состояния, но обычно при этом очень многие параметры, как например $K'_T$, фиксируются, что приводит к "притягиванию за уши" остальных параметров.
Расчёты по приведённым данным.
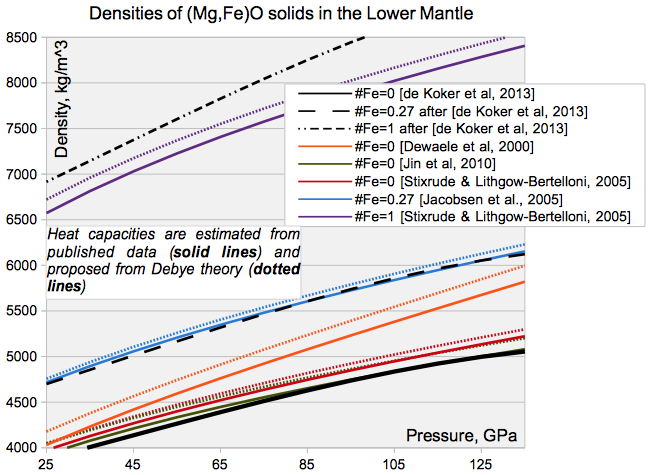
В прошлом посте я так и не привёл графика собственных расчётов по приведённой схеме. Время это исправить. В качестве примера, график для самого простого вещества - периклаза (Mg,Fe)O с разными пропорциями железа-магния (#Fe = Fe / (Fe + Mg), 0 ≤ #Fe ≤ 1)
Цветными пунктирами показаны теплоёмкости из теории Дебая, сплошными линиями - расчёт по данным из статей. Разница обусловлена в первую очередь тем, что авторы далеко не всегда публикуют все данные, необходимые для полного вопроизводства расчёта теплоёмкости. Так, разница иногда достигает 25% (!). Спасает только то, что вклад термального давления довольно-таки мал.
Чёрной линии показана базовая используемая мной модель для чисто магнезиального члена, пунктирами - расчёты для разных содержаний железа. В общем, в условиях небольших содержаний железа модели показывают довольно-таки согласованные значения (не считая особо оригинальной [Dewaele et al., 2000]).
Сравнение с альтернативными источниками.
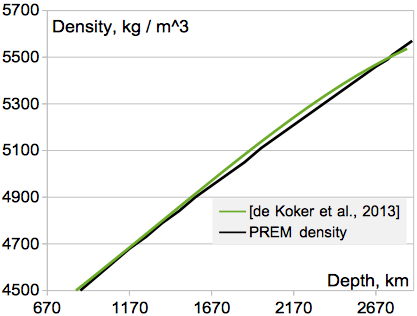
Сравнение рассчитанного профиля (уже зелёный) и данными глубинной геофизики (чёрный), по-моему, оставляет только один главный вывод: мы не просто понимаем, но можем великолепно промоделировать то, что происходит в недрах планет.
В настоящее время существуют возможности определения фазового и структурного состава вещества в момент прохождения волны. Более того, есть возможности получения развёртки во времени некоторых параметров среды, включая кавитацию - формирование пустот внутри материала (см. напр. тут). Более подробная статья, посвящённая изменениям материалов в условиях ударных волн, есть тут (хотя, конечно, их очень и очень много).
Использование указанных параметров для получения уравнения состояния вещества.К слову, если советские данные в основном не лежат в открытом доступе, то с американскими таких проблем нет, и я с большим удовольствием их читаю, поскольку обычно написаны они весьма неплохим языком, как например "Some physics of the Gruneisen parameter".
В своём прошлом посте я постарался подробно рассказать об основных особенностях уравнения состояния вещества. В статье фигурировало довольно много параметров, измерение которых осталось за кадром. Сейчас же, после обращения к экспериментальным методам, можно сказать и о методиках измерения параметров.
Главное допущение. В момент прохождения ударной волны у нас есть два состояния вещества - до сжатия и после сжатия, между которыми проходит фронт волны, по многим свойствам аналогичный фазовой границе. Поэтому, исходя из уравнений сохранения импульса и энергии мы можем вывести несколько базовых формул.
Главная формула - это уравнение Ранкиля-Гюгонио (Rankine–Hugoniot):
\[\rho_H (U_s - u_p) = \rho_o U_s\]
которое связывает плотность вещества после сжатия $\rho_H$, до сжатия $\rho_0$ со скоростями ударной волны $U_s$ и скоростью частиц $u_p$. Скорость частиц - это скорость перемещений атомов вещества, непосредственное измерение которой представляет значительную сложность.
Поскольку скорость перемещения частиц вещества ударной волной превышает таковое в звуковой волне, возникает переуплотнение вещества. Следует отметить, что скорость звука также обязательно равна скорости перемещения молекул.Решение уравнения относительно скорости частиц, предложенное [Ahrens, 1987] представляет собой это наглядное простое выражение:
Так, в воздухе скорость отдельных атомов составляет порядка 500 м/с (распределение Масвелла подсказывает), а скорость звука в полтора раза ниже.
То есть скорость ударной волны, скорость частиц и скорость звука - это три разные величины, связанные друг с другом только через "третьи" свойства вещества.
\[ u_p = u_{fp} + \frac{C_{0,fp} + U_s\frac{\rho_{0}}{\rho_{0,fp}}}{2S_{fp}} - \sqrt {\left(\frac{C_{0,fp} + U_s\frac{\rho_{0}}{\rho_{0,fp}}}{2S_{fp}}\right)^2 + \frac{ \frac{\rho_{0}}{\rho_{0,fp}} U_s u_{fp} }{S_{fp}} }\]
где $u_p$ - скорость частиц, $u_{fp}$ - скорость flyer plate, $U_s$ - скорость ударной волны, $\rho_{0,fp}$, $\rho_{0}$ - плотность flyer plate и вещества мишени в нормальных условиях, $S$ и $C_0$ связаны между собой уравнением:
\[ U_s = C_0 + Su_p \equiv \sqrt {\frac{K_{S,0}}{\rho_{0}}} + \frac{K_S' + 1}{4}u_p \]
где $K_{S,0}$ - изоэнтропный объёмный модуль сжатия, а $K_S' = \frac{dK_S}{dP}$ (подробнее в предыдущем посте).
Далее, мы можем из пространства скорости ударной волны и скорости частиц перейти к пространству давления-объёма, то есть термодинамических параметров:
\[ u_p = \sqrt{(P_1-P_0)(V_0-V_1)} \]
\[ U_s = V_0\sqrt{\frac{P_1-P_0}{V_0-V_1}} \]
Также можно перейти к внутренним энергиям (обозначаются E или U, здесь изложение по [Mosenfelder et al., 2007]). Есть базовая формула, связывающая разницу внутренних энергий вещества в шоковом состоянии (индекс $H$) и вещества на изоэнтропе (при адиабатическом сжатии, то есть, грубо говоря, без обмена теплом, индекс 0):
\[ \Delta E_H = \frac{P_H}{2} \left( \frac{1}{\rho_0}- \frac{1}{\rho_H} \right)\]
Изоэнтропа же определяется уравнением статического сжатия (т.е. уравнением, связывающим плотность только с давлением, без изменения температуры), например, то уравнение Birch-Murnaghan, о котором я говорил в прошлом посте. Для него изменение внутренней энергии переписывается в виде:
\[ \Delta E_S = \frac{9 K_{S,0}}{2\rho_0} \left( \frac{(\rho_H/\rho_0)^{2/3}-1}{2}\right)^2 \left( 1 + (K'_{S}-4) \left( \frac{(\rho_H/\rho_0)^{2/3}-1}{2}\right) \right)\]
Так как нам надо от изоэнтропы перейти к гюгониоте (так называется график ударного сжатия в P-V координатах), то надо к этой $\Delta E_S$ добавить энергию перехода (этот подход вместе с допущением о зависимости параметра Грюнайзена $\gamma$ только от давления) обобщается в теории Mie-Gruneisen):
\[ \Delta E_V = \frac{P_H - P_S}{\gamma \rho_H} = \frac{P_H - P_S}{\gamma_0 (\rho_H/\rho_0)^q \rho_H}\]
Теперь, если мы просуммируем эти энергии и добавим энергию возможных фазовых переходов $\Delta E_{tr}$ (что делается просто как разность энергий образования веществ), мы получим:
\[ \Delta E_H = \Delta E_S + \Delta E_V
Совокупность этих уравнений позволяет создать термодинамическую взаимосогласованную расчётную базу.
Термодинамические и реологические свойства веществ
Итак, в вышеприведённом тексте у нас фигурировали (помимо состояния вещества при заданных параметрах $\rho_0-P_0-T_0$) модуль объёмного сжатия $K_S$, его производная по давлению $K_S'$, параметр Грюнайзена $\gamma$ (внимание! это не отношение теплоёмкостей из теории газов!!), параметр Грюнайзена второго порядка $q$.
Модуль объёмного сжатия и его производная устанавливаются по вышеприведённым уравнениям.
Параметры Грюнайзена $\gamma$ и $q$ устанавливаются, если установить несколько гюгониот при постоянном объёме (но разной внутренней энергии, напр. [Mosenfelder, 2007b]).
Количество переменных для поиска нередко сужают, принимая некоторые параметры фиксированными (исходя из свойств подобных веществ или предыдущих исследований). В принципе, с учётом того, что возможных параметров для варьирования достаточно много, остаётся достаточно степеней свободы.
Зная эти параметры, можно рассчитать изотермический модуль сжатия $K_T$ и его производную по давлению $K_T'$ (при необходимости и начилии данных- и $dK_T/dT$), которые и нужны для уравнений состояния (см. прошлый пост).
Последний необходимый параметр, который нам нужен - это коэффициент термического расширения $\alpha$ или теплоёмкость $C_V$. Они абсолютно взаимозаменяемы при известных вышеперечисленных, как следует из формулы:
\[ C_V = \frac{\alpha K_T}{\gamma \rho} \]
Есть несколько подходов.
Непосредственная калориметрия в условиях сверхвысоких давлений и температур не реализуема. Во всяком случае, не видел я таких работ.
Простой и совсем плохой - это взять теплоёмкость при низких давлениях и использовать её.
Второй и немного получше - это использовать, в конечном счёте, теплоёмкость по Дебаю. В принципе, при известных скоростях звука в среде это получается довольно адекватный метод. Но только если они известны.
Третий метод, который уже основан на измерениях. Это измерение коэффициента температурного расширения. Это возможно проделать в качестве довольно рутинной процедуры в описанной выше установке с алмазными наковальнями. Метод дифракции рентгеновских лучей (X-ray diffraction) позволяет провести непосредственное измерение объёма элементарной ячейки кристаллической фазы in situ, т.е. в условиях эксперимента (напр. [Mao et al., 2011]).
PS: алмазные наковальни, теоретически, позволяют также калибровать уравнения состояния, но обычно при этом очень многие параметры, как например $K'_T$, фиксируются, что приводит к "притягиванию за уши" остальных параметров.
Расчёты по приведённым данным.
В прошлом посте я так и не привёл графика собственных расчётов по приведённой схеме. Время это исправить. В качестве примера, график для самого простого вещества - периклаза (Mg,Fe)O с разными пропорциями железа-магния (#Fe = Fe / (Fe + Mg), 0 ≤ #Fe ≤ 1)
Цветными пунктирами показаны теплоёмкости из теории Дебая, сплошными линиями - расчёт по данным из статей. Разница обусловлена в первую очередь тем, что авторы далеко не всегда публикуют все данные, необходимые для полного вопроизводства расчёта теплоёмкости. Так, разница иногда достигает 25% (!). Спасает только то, что вклад термального давления довольно-таки мал.
Чёрной линии показана базовая используемая мной модель для чисто магнезиального члена, пунктирами - расчёты для разных содержаний железа. В общем, в условиях небольших содержаний железа модели показывают довольно-таки согласованные значения (не считая особо оригинальной [Dewaele et al., 2000]).
Сравнение с альтернативными источниками.
Сравнение рассчитанного профиля (уже зелёный) и данными глубинной геофизики (чёрный), по-моему, оставляет только один главный вывод: мы не просто понимаем, но можем великолепно промоделировать то, что происходит в недрах планет.
Сопоставление плотности, полученной из данных Molecular Dynamics (про это был отдельный пост), и плотностей, полученных геофизикой, для нижней мантии Земли.
Вывод, думаю, можно сделать из всего этого только один. Современная наука и технология позволяют не только получать вещества в экстремальных условиях, но и эффективно предсказывать их свойства.





Комментариев нет:
Отправить комментарий