В предыдущей статье я уже описывал, то, чем я занимаюсь. Вкратце, мне была выдана в зубы статья [de Koker et al., 2013], которые провели моделирование на суперкомпьютере вещества нижней мантии и получили диаграмму плавления вещества (кому интересна полноразмерная картинка, обращайтесь):
Также они привели несколько десятков графиков для удельного объёма и внутренней энергии вещества. От меня было необходимо сделать некую программу, которая могла бы плавить вещество по предложенной модели.
В предыдущей статье я описал приближения, благодаря которым у меня получилось рассчитать диаграмму плавкости для произвольного давления между 24 и 136 ГПа (в условиях Земли это глубины от 660 до 2900 км), и даже расширить область применимости до ~250 ГПа.
Теперь же мы поговорим о реализации.
Часть I. Плавление и кристаллизация.
Вот так можно параметризовать параболическими функциями фазовую диаграмму для давления 136 ГПа:
Это для нулевого содержания железа. Если же его больше нуля, то его воздействие на температуру можно ввести линейной поправкой k на коэффициент r в уравнении парабол (подробнее в предыдущем посте):
T = px2 + qx + (r - x(Fe)*k)
По факту, речь идёт о 15 градусах на каждый процент железа.
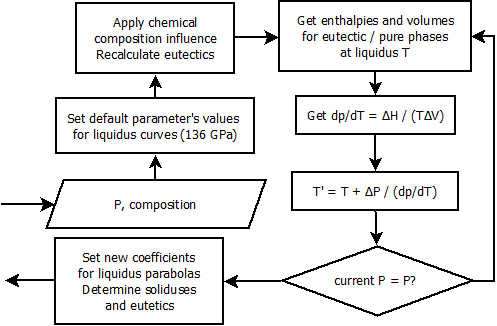
Пользуясь изложенными в предыдущем посте ухищрениями с уравнением Клаузиуса-Клапейрона, параболы могут быть пересчитаны для любого давления:
Пользуясь изложенными в предыдущем посте ухищрениями с уравнением Клаузиуса-Клапейрона, параболы могут быть пересчитаны для любого давления:
После этого пишется функция, которая бы, в условиях заданных температуры и давления, могла бы, посредством волшебного пенделя в виде порции теплоты, нагреть и поплавить вещество.
Для этого нам понадобится теплоёмкость CP и скрытая теплота (энтальпия) плавления L веществ. Они могут быть посчитаны довольно просто:
CP = (dH / dT)P
L = HL - HS
Где H, HL и HS - это энтальпии образования любого вещества, расплава и твёрдой фазы соответственно.
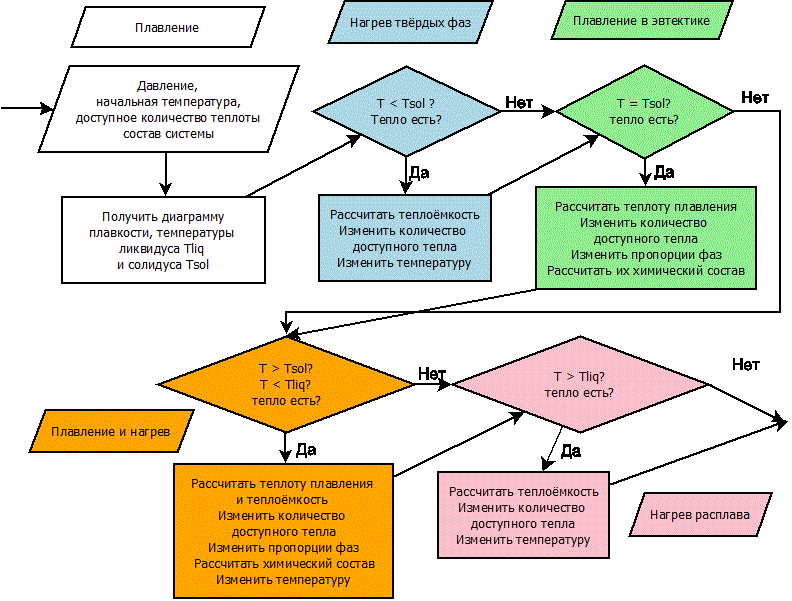
После этого в программиста необходимо залить примерно 5 литров кофе, и он выдаст функцию, которая это будет рассчитывать по примерно такой схеме:
Соотвественно, каждая пара ромбик-прямоугольничек образуют цикл с пошаговым расчётом, так как указанные выше параметры имеют свойство изменяться в зависимости от температуры, химического состава и пропорций фаз
Так как "пендель" означает, вообще говоря, в переводе с немецкого на русский, маятник, тепло ещё умеет и убывать. Потому нам потребуется аналогичный модуль для расчёта кристаллизации вещества. Для этого в программиста надо влить ещё 2 литра кофе. И ещё литр на отладку и за вредность.
Часть II. Интегрирование в имеющийся код.
Самое интересное только начинается.
Хотя изначально предполагалось из статьи [de Koker et al., 2013] взять только диаграмму плавления и теплоты плавления, но коль пошли такие пироги с теплоёмкостями и прочей ересью, можно взять не только теплоты плавления, но и ересь.
Потому сначала пишется несколько функций, которые подставляются в имеющиеся подпрограммы, занимающиеся собственно плавлением и кристаллизацией вещества.
А потом пишется ещё десяток функций, которые могли бы в основную программу возвращать и иные термодинамические параметры, которые бы использовались в других модулях. Причём они должны обеспечивать всё взаимодействие с программой, да ещё и так, чтобы все динамические переменные обнулялись и т.д.
И, естественно, пишется ещё десяток технических функций, которые пересчитывают туда-сюда химические составы, давления и прочие мелочи.
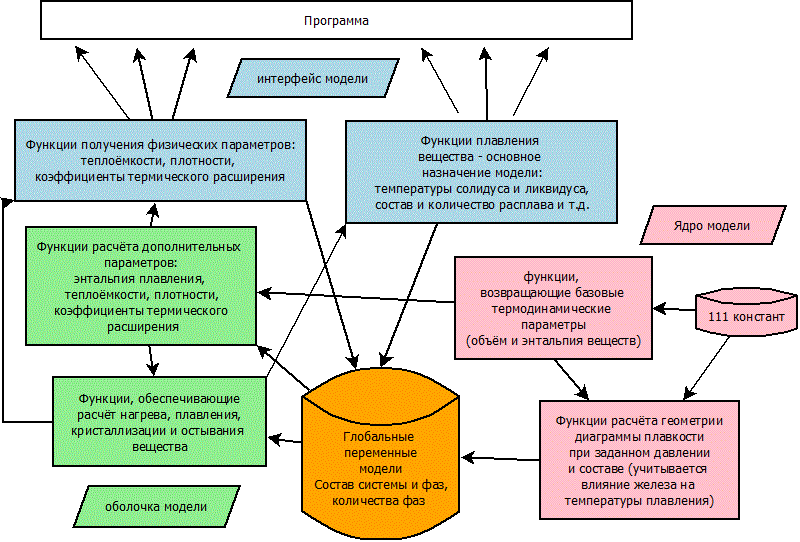
А на выходе получается вот такая структура:
Соответственно, хвостик стрелочки указывает на то, что даёт данные, нужные тому, на что указывает головка стрелочки. И всякий раз идти надо до конца - то есть пройтись по абсолютно всем функциям до блока "111 констант".
В принципе, если ещё расписать все функции наподобие плавления, я смогу продавать настольную игру для детей младшего студенческого возраста "расплавляй-ка!"...
Вообще, всё, что было проделано выше - это полная ересь и так жить нельзя. Если подумать, то всё получилось по такой схеме:
- Сначала были предложены квантово-механические уравнения типа волновой функции Шрёдингера
- Потом их никто не смог решить, и была предложена куча параметризаций, чтобы сделать вид, что их решили.
- Потом данные этой параметризации были экстраполированы на глубины в тысячи километров.
- Потом по ним как-то посчитали (с ещё большими округлениями и погрешностями, чтобы компьютер хоть когда-то это досчитал) состояния веществ.
- Потом пришёл я и
всё испортилнавёл абсолютно высосанные из пальца интерполяции. - А потом по ним я ещё и что-то считаю для тех условий, для которых вообще не было сделано расчётов. Круто?
Практически единственным параметром, который мы можем протестировать - это плотность пород. Она приходит из данных глубинной сейсмики, редких данных по ксенолитам и экспериментальной петрологией (см. у меня тут и тут, а лучше - в хорошей статье [Kaminsky, 2012]). Одна из наиболее известных моделей - Preliminary Reference Earth Model (PREM). Некоторые данные этой модели можно посмотреть например тут, а сама статья, имеющая по данным Google, 6047 цитирований, лежит вот тут.
Здесь для глубин меньше 660 км смотреть не надо. На этой глубине происходит перекристаллизация периклаза и пироксена со структурой перовскита в рингсвудит (полиморф оливина), гранат и пироксен), потому эта диаграмма отражает свойста метастабильных фаз. Следует отметить, что физический смысл не теряется, поскольку и алмаз существует вне поля своей стабильности, где его по законам термодинамики быть не может никак и никогда.
А вот для глубин >660 км мы видим действительно потрясающее согласование теории и практики: погрешность в первые проценты. С учётом того, что PREM - это только "среднее по больнице", это блистательное подтверждение работоспособности изложенной выше схемы.
Надо отметить, что, поскольку плотность вещества зависит и от температуры, то полученное согласование неявно подтверждает и остальные допущения и параметризации.
Сам, честно сказать, очень удивился.
Как было сказано выше, программа рассчитывает и некоторые дополнительные термодинамические параметры.
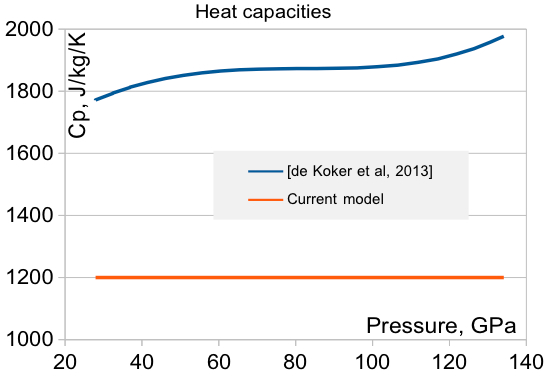
Теплоёмкости веществ:
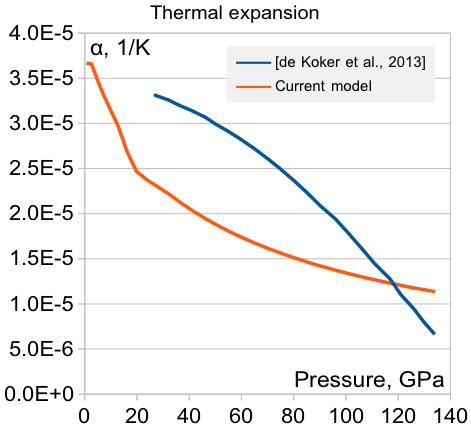
И коэффициент термического расширения α:
α = 1/V (dV / dT)P
То есть, хоть и величины того же порядка, что и были, но всё-таки значения отличаются.
PS: диаграммы, приведённые в этой статье, нарисованы в очень хорошей бесплатной программе Dia Diagram Editor.



Комментариев нет:
Отправить комментарий