Давления в недрах Земли

Основная проблема петрологии - установление глубин формирования пород. Наиболее актуальной она становится в приложении к геодинамике и процессам формирования ультравысокобарных комлексов (UHP terrains).

В этом посте я попробовал дать краткое описание связи термодинамического давления с реальным давлением в горных породах, и соотношение последнего с литостатическим.

 "Давление подразделяется на  всестороннее (литостатическое),

обусловленное массой вышележащих горных пород, и

стрессовое, или одностороннее, связанное с тектоническими

направленными движениями." - [Короновский, Якушева, 1991]

Постановка задачи:

Для понимания истории нашей планеты (как глобального процесса) и истории отдельных геологических тел (среди которых могут быть и месторождения полезных ископаемых) необходимо уметь отвечать на простой вопрос: при каких услових сформировалась та или иная порода. Одним из таких условий является давление. В случае магматических и метаморфических пород оно может достигать многих тысяч атмосфер.

Почему возможно вообще ответить на этот вопрос?

Геолог имеет дело с куском породы, в котором есть минералы. Если мы поместим эту породу под некоторое давление и температуру, через некоторое время в ней будет достигнуто равновесие.
Естественно, стоит только изменить эти параметры, порода будет стремиться вернуться в низкотемпературные и низкобарные условия. Но стремиться - не значит успеть (думаю, вы понимаете бытовые аналогии). Кинетика этого процесса определяется во многом скоростями диффузии атомов в кристаллических структурах.
Одна из первых предложенных формул - это [Dodson, 1963]. Возможно, она слишком упрощённая, но зато даёт представление о взаимосвязи величин Она связывает время уменьшения коэффициента диффузии до пренебрежимых скоростей $\tau$ с температурой $T$, энергии активации диффузии $E$, универсальной газовой постоянной $R$ и скоростью охлаждения $dT/dt$:
\[ \tau =  -\frac{RT^2}{E}\left(\frac{dT}{dt} \right)^{-1} \]
Таким образом, при достаточно большой скорости остывания системы происходит так называемое закаливание - то есть система не успевает перейти в равновесное состояние. К слову, процесс варки стекла (которое в окнах, например) - это как раз таки закаливание силикатного расплава. 
Ещё один важный параметр, температура закрытия системы (то есть далее скорость диффузионных процессов пренебрежимо мала), определяется формулой:
\[ T_c = \frac{R}{E \ln(A\tau D_0 / a^2)} \]
где $A$ - это некая константа, следующая из геометрии системы и особенностей веществ, $D_0$ - коэффициент термической диффузии ($D=D_0 \exp(-E/R/T)$),  $a$ - характерный размер зёрен фаз.

Таким образом, из теории диффузии непосредственно следует шанс того, что высокобарные высокотемпературные парагенезисы (сочетания совместно образованных минералов) могут дожить до исследователя.

Как возможно ответить на этот вопрос?

В термодинамике давление появляется в известной формуле:

\[ U = TS - PV + \sum_i \mu_i M_i \]
откуда затем перекочёвывает во все остальные формулы (стандартная нотация для внутренней энергии, температуры, энтропии, давления, температуры, химического потенциала и количеств веществ).
Применив чёрную магию некоторые другие термодинамические соотношения

\[ \Delta G_{T,P} = 0 = \Delta H_{T_0,P_0} - T\Delta S_{T_0,P_0} + P\Delta V + RT \ln K_D \]
Путём простейших арифметрических действий, можно получить выражения для давления типа:\[ P = - \frac{ \Delta H_{T_0,P_0} - T\Delta S_{T_0,P_0} + RT \ln K_D}{\Delta V} \]
Когда мы пытаемся применить эту формулу к реальной жизни, ничего не получается, можно получить какие-то коэффициенты. В качестве примера такого уравнения можно упомянуть равновесие граната и пироксена ($K_D$ - параметр, напрямую рассчитываемый из химического состава фаз):
\[ P_{MPa} = -73179 + 228 T + \frac{RT \ln K_D}{0.66} \]
Такие простые уравнения создают большой соблазн для массовых и беспощадных расчётов.

Одним из очень красивых и простых примеров получаемых реконструкций является такая вот картинка из статьи [Moulas et al., 2013]. На ней изображён P-T path - график изменения температуры и давления в породе, построенный исходя из расположения зёрен-включений разных давлений и температур в единичном зерне граната (в котором мы можем однозначно говорить о последовательности смены условий по мере роста зерна граната-хозяина):

Слева - зерно граната со схемой расположения включений кварца и коэсита. Более высокобарный коэсит находится по периферии зерна, а низкобарный кварц - вокруг, что даёт возможность однозначно говорить о последовательности смены условий (по данным [Parkinson, 2000]).

Что делают с ответом?

Давление хорошо, но глубины лучше: душа геология - наука о пространственном расположении пород, требует чего-то более конкретного, чем какое-то давление. Например, перемещение в пространстве блока породы. Временные отметки даёт нам геохронология, а вот что делать с глубинами?

Когда хочется чего-то большего и немедленно, на помощь приходит школа. Так, из школы мы знаем формулу для расчёта давления под столбом вещества высотой $z$ (гидростатическое давление, которое приличия ради называют геологи называют литостатическим):
\[ P = \rho g z \phantom{MM} \Longrightarrow \phantom{MM} z = \frac{P}{\rho g} \]
И тотально подавляющее большинство статей, рисующих так называемые P-T path - графики изменения температур и давлений, при которых была порода, во времени, используют именно эту формулу для перерисовки графика в координаты глубин!
И именно на основе этого графика глубин изобретаются модели, которые объясняют получаемый ультра-быстрый подъём пород из глубин Земли к поверхности (ultra-high exhumaton rate), который является одной из больших проблем современной геологии. В частности, потому, что существующие геодинамические модели не могут "позволить" таких высоких скоростей вертикального перемещения пород - даже с учётом эрозии.
 
Есть только один вопрос - работает ли эта формула в реальной Земле? Верны ли эти выводы об ультра-быстром подъёме пород?

А был ли мальчик?

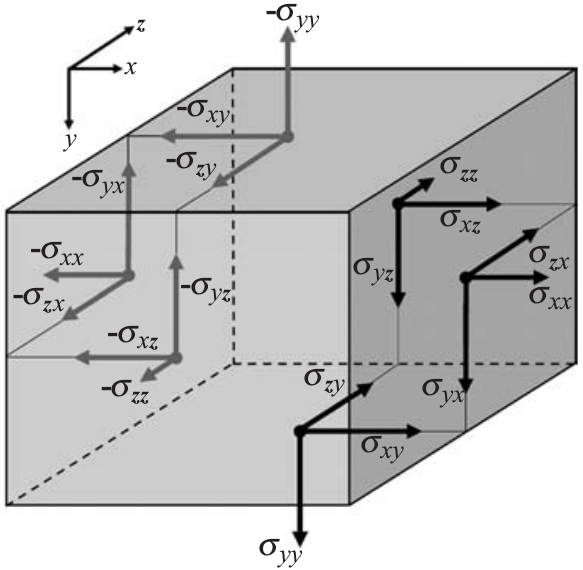
Механика сплошных сред говорит, что каждый единичный объём породы может испытывать следующие компоненты напряжений $\sigma$, имеющих размерность давления (рис. из [Gerya, 2009]):

Каждая "сторона" испытывает одно перпендикулярное ей напряжение (сжатие или растяжение) и два сдвиговых. Давление же (которое и "подставляется" в вышеприведённые формулы) определяется как:
 \[ P = -\frac{\sigma_{xx}+\sigma_{yy}+\sigma_{zz}}{3} \]
Соответственно, в условиях гидростатического равновесия выполняются равенства:
 \[ \sigma_{ii} = -P; \phantom{MM} \sigma_{ij} = 0,\phantom{i}i\neq j  \]

Эти условия будут выполняться только в полностью релаксировавшей среде. В любой тектонически активной провинции (а любой т.н. ультравысокобарный комплекс и происходит из такой зоны) будут наблюдаться отклонения.

Формула $P=\rho g z$ весьма хороша в практических целях - например, для совсем небольших глубин. Она будет отлично работать и на абсолютно мёртвой планете - без какой-либо геодинамики сейчас и в прошлом. Понятно, что идеальная сферическая конь планета в вакууме не существует (и это даже не парадокс).

Насколько всё плохо?

Буду краток. Всё очень плохо.

Наиболее простой метод изучения возможных сверх- и недодавлений (tectonic under- and overpressure) - это численное моделирование. Основанное на фундаментальных физических принципов, оно хоть (пока) и не учитывает всех возможных процессов (например, дегидратация минералов при высоких давлениях и прочие специфические явления), оно даёт реалистичную картину распределения напряжений.

На уровне отдельных зёрен:
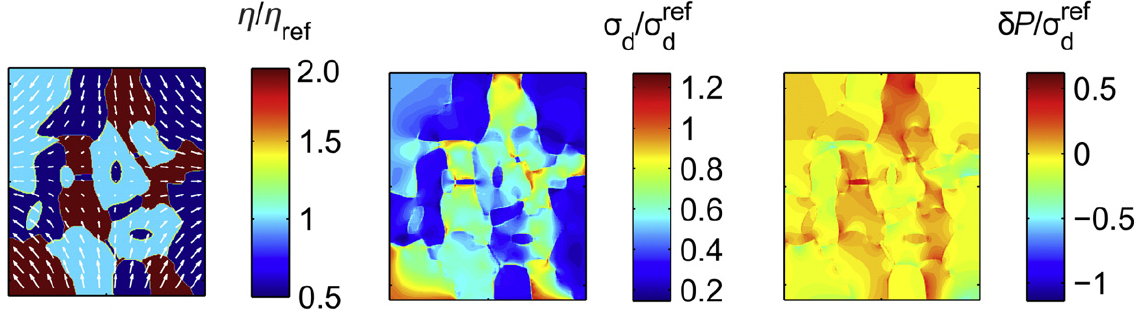
2D-моделирование, проведённое [Tajčmanová et al., 2015], показывает, насколько разное давление развивается в отдельных зёрнах при сдавливании породы с боков:

На рисунках $\sigma_d = \sigma_{xx}-\sigma_{yy}$, то есть разница приложенный напряжений (условно говоря, давлений) в разных направлений. Соответственно, индекс $\sigma_d^{ref}$ означает приложенную разницу напряжений, а $\sigma_d$ - наблюдаемую в зёрнах, а $\vardelta P$ - вариацию давлений в "образце".

На уровне земной коры:
Наверное, самым показательным примером будут иллюстрации из статьи [Schmalholz, Podladchikov, 2013]. В данной статье авторы изучали распределение тектонического давления (разность полного и литостатического давлений) при приложении такого напряжения ( сдавливания с боков) к разрезу литосферы, при котором она сокращается на 15%:

Диаграмма показывает, что тектоническое "сверх"-давление может составлять от -30% до +70% от приложенного напряжения в зависимости исключительно от расположения конкретного блока породы в пространстве.

В общем же случае, в зависимости от геометрии модели и от системы приложенных напряжений (оставаясь в поле "реалистичных" напряжений), тектоническое сверх давление может быть от -100% до +100% от литостатического давления и достигать величин в первые гигапаскали [Gerya, 2014], [Gerya, 2015 (в печати)].

Несколько примеров "из природы"

Кварц в массиве Кокчетав

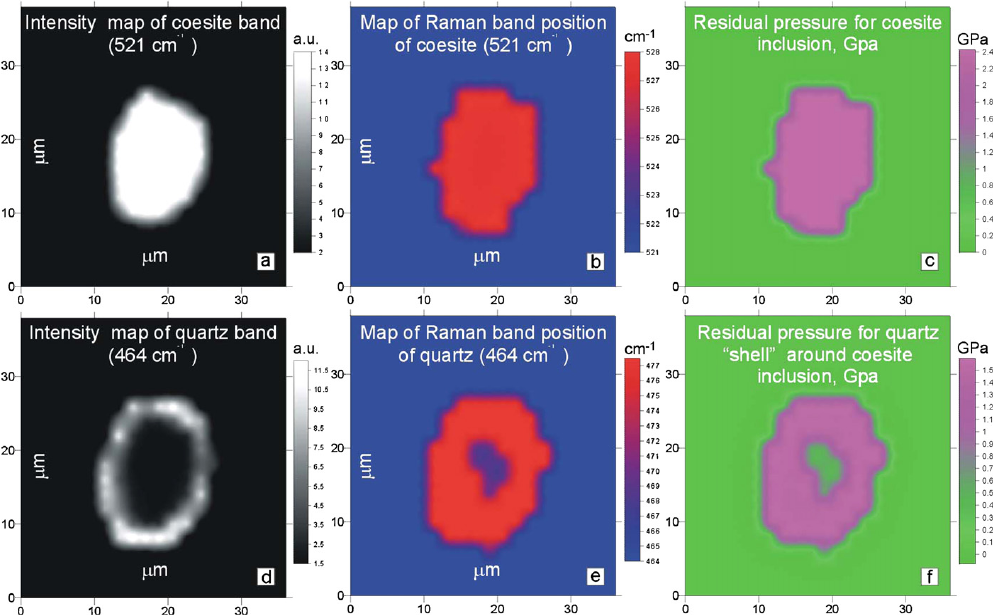
[Korsakov et al., 2007] использовали смещение пиков в рамановской спектроскопии для измерения остаточного давления в кварце и коэсите - зёрнах-включения в гранате.

Небольшая справка: высокобарный полиморф кварца, коэсит, может существовать только при очень высоких давлениях. При понижении давления он практически всегда переходит в кварц. Однако в породах массива Кокчетав были найдены включения коэсита в гранате, часто окружённые так называемым палисадным кварцем.

Обратите внимание на измеренные сверхдавления: в образце, находящемся в поверхностных условиях, они достигают 1.5 ГПа!

В обширном обзоре, проведённом в статье [Moulas et al., 2013], приведены значения подобных остаточных давлений в 3 и более ГПа (!), что соответствует "литостатическим" глубинам порядка 100 км (!!!).

Как неоднородность приложенного давления влияет на фазовые переходы

В уже упомянутой работе [Tajčmanová et al., 2015] приведены положения фазовой границы кварц-коэсит при $\sigma_d = \sigma_{xx}-\sigma_{yy}$ в 1 кбар:

Казалось бы, расчёт и расчёт - мало ли что можно посчитать. Одна проблема - точки показывают экспериментальные данные. И, хотя совпадение и не 100%, тем не менее, необходимо признать: да, это работает.

И, внимание! Даже такая крохотная "анизотропия" давлений, как 1 кбар, приводит к смещению фазовых равновесий на десятки килобар (!!!).

Совмещение PT-path и реальной тектоники

В заключение хотелось бы показать потрясающий результат [Pleuger, Podladchikov, 2014]. В работе показано соотношение петрологически определённого давления (по термодинамическим соотношениям), литостатического давления и глубин для Адульского надвига (Adula nappe) в центральных Альпах.

В рамочках, сверху вниз: глубина (км), литостатическое давление (ГПа, определение по простейшей формуле), полное (реальное) давление (ГПа, определение по минеральным равновесиям), отношение полного и литостатического давлений.

Таким образом, сочетание численного моделирования и петрологических данных позволило реконструировать всю сложную геодинамику региона.

Заключительные замечания

1. Термодинамическое давление, измеренное для пород из зон активной геотектоники, не является прямым показателем глубин.
2. Реальное давление (=термодинамическое) является суммой литостатического и тектонического давлений, причём может быть как больше, так и меньше литостатического.
3. Горные породы могут содержать включения, до сих пор находящиеся под ультравысокими давлениями; вариации давления в пределах образца могут достигать гигапаскалей даже спустя миллионы лет после его образования: кристаллическая решётка минералов его выдерживает
4. Фазовые переходы, особенно связанные с большим изменением (увеличением) объёма, как например плавление, могут в значительной мере контролироваться повышением давления в ходе этой реакции. Условно говоря, система будет определяться не (P,T) параметрами, а (V,T).

Картинка в начале поста с сайта Университета Орегона.