log(exp(...))

Столкнулся с отличным примером того, как работает машинная точность, и какие от этого могут быть проблемы.

A good example on how does computer precision work and what are the possible consequences.

Есть такие понятия - прямая и обратная задача. Прямая задача - это, при знании устройства чего-то предсказать, как оно работает. Например, если знать, что в консервной банке лежат монеты, можно предсказать, что они будут греметь. Обратная задача - это по звону монет понять, что там монеты (а не подшипники) и оценить их номинал. Прямая задача куда понятнее, а обратная задача - это то, с чем сталкиваются во многих разделах науки. Например, именно к обратным задачам сводится основная работа в геофизике, когда по скоростям сейсмических волн надо понять, что у планеты внутри.

There are two important concepts: direct (or forward) and inversed problems. Direct task is to propose the effect if you know the constituents. For example, if you have a can full of coins, you can predict that it is pretty noisy falling down on floor. The inverse problem is to estimate what was actually falling down on floor and how much money it had inside. The forward problem seems to be much easier, but the latter one is something scientists faced with. For example, geophysicists try to reveal what's inside the planet by seismic tremor recorded at the Earth's surface.

Когда неизвестных становится очень много, а уравнения связи - чересчур сложны, оказывается проще посчитать возможные варианты и выбрать наиболее подходящий. Считать совсем всё невозможно, и используют подход Монте-Карло - случайным образом выбрать много-много вариантов, а потом взять подходящий. Его дальнейшее развитие - это цепи Маркова, когда алгоритм сам сравнивает, насколько расчёт похож на правду, и, в случае, если разница невелика, выбирает следующий вариант где-то рядом. Самим же выбором управляет случайность: случайным образом находится следующий вариант, случайным же образом определяется, принимать ли его или не принимать. Это похоже на лабиринт со множеством дверей. Часть из них тугие, а часть - нет. И у вас в руках игральная кость. Вы кидаете - и она говорит, с какой силой вы можете пытаться открыть дверь. Чем проще пройти, чем больше ваши данные похожи на нужные, тем больше вероятность, что вы пройдёте. Но всегда есть шанс, что вы пройдёте через очень тугую дверь. А вдруг - там было не решение, но всего лишь его подобие? А там, за тугой дверью, будет правильный ответ.

Есть даже специальная уловка на случай, если правильный ответ будет за слишком тугой дверью. Метод параллельного темперирования (аааа, в переводе это звучит ужасно) даёт некоторым этим человечкам, ходящим по этому лабиринту, возможность открывать почти любые двери, а потом телепортировать туда обычного человечка, который уже и будет изучать окрестности. 

Более научное объяснение на примере последнего метода. Есть графит и алмаз. На поверхности Земли термодинамически устойчив только графит, но алмаз не может перейти в него, если его не нагреть (потому что высокая энергия активации для перехода, это называется метастабильностью). Но, предположим, мы, кроме алмаза, углерода не видели, и что будет, если его нагреть, не знаем (да, мы чуть-чуть уже пообжигались и просто прокаливать алмаз не хотим). Метод ПТ позволяет запустить несколько расчётов при разных температурах (да, темперирование - это о температуре, а не времени, хотя бы потому что у меня мороз по коже от того, как это ужасно звучит), так что даже если мы начнёт расчёт со структуры алмаза (начальная гипотеза), одна из цепочек расчёта перешагнёт в графит и перетащит туда остальных, так что наше итоговое предсказание будет верным.

As soon as number on unknowns become very very big, it becomes easier to compute the possible cases and choose the most affordable one. However, it's impossible to compute absolutely all the cases. Monte-Carlo method says, you may calculate only a lot of randomly chosen cases and then you may hit a good option. The further development of this approach is so-called Markov chain method: each next variant is tested on how close is it to the solution, and then the program decides, whether it should be accepted or not. The decision is based on random numbers: a random value decides where should you move, and then random value tells are you allowed to actually proceed there. That's like a labyrinth with hundreds of doors. Some of them are stiff, while some are really easy. And you drop a dice each time to learn how much force can you apply to the door. So more often you pass easy doors, but sometimes you might go though a hard one.  

There are even hints to go to another part of the labyrinth. Some of lost-in-the-doors-guys are given with special permissions to pass through almost any door (this is called parallel tempering). And they know the spell of teleport, so that they can move any other ordinary guy to look for a solution around.

More scientific explanation for the latter technique. Let's take graphite and diamond. Only one of them is thermodynamically stable on the Earth's surface, while diamond needs to be heated to change its internal structure to graphite. That's called high activation energy, and diamond is known to be a metastable phase - it may not overcome the trespass. Let's imagine we live in the Earth's lower depths and we had never seen any single piece of carbon besides the diamond. And we want to learn what will happen to it during heating before doing it (that's pretty smart, isn't it?). Parallel Tempering allows to run a number of chains under different temperatures (yes, that's about temperature not time) and take a look what happens. High-temperature dudes feel no barrier of activation energy, so they will easily go to graphite and bring some low temperature guys to sample it.

Может показаться очень странным такой подход, когда серьёзные вещи доверяются случайности. Побеждает статитистика. Простейшие модели пробуют десятки тысяч случаев. И статистика умеет указывать на то, что что-то идёт не так. Сейчас я расскажу об одной из функций, которая очень хорошо показала этой свойство.

One may say this is not robust to trust some randomly selected values. Statistics matters. The simplest models try thousands of cases. And statistics can point you out that something goes wrong. I'm going to tell now how does it work.

\[ f(x,y,z) = \exp\left(-\frac{x^2+ y^2+ z^2+(x\cdot y\cdot z) ^2 -20\cdot x \cdot y \cdot z}{2}\right) \]

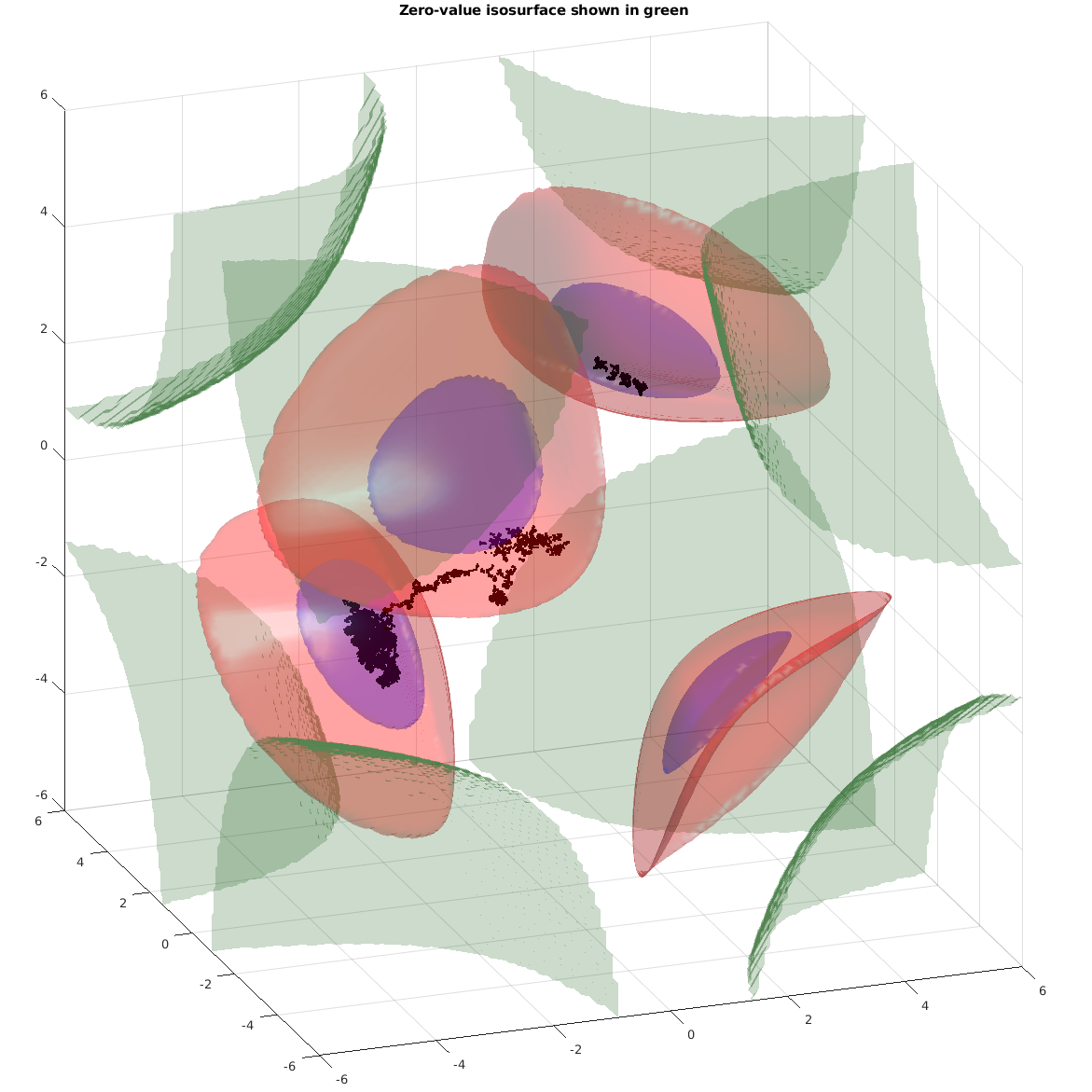
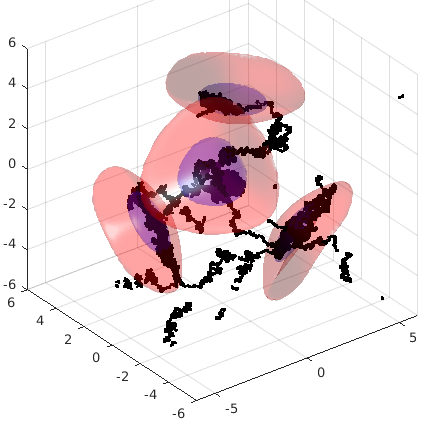
Это простейшая тестовая функция, которая показана на первой картинке в начале поста. Красноватым показаны интересные области, а фиолетовым - очень интересные. Мы должны сделать так, чтобы, начав в произвольной точке (например, в начале координат), мы прошли по всем этим несвязным областям. Чёрный "червяк" показывает путь, пройденный одной из цепей Маркова в этом пространстве

This simple test function is shown on the very first image in this post. Reddish are areas of increased interest, and violet are very interesting regions to be sampled. We must start at some random point and go around all the regions. Black "worm" shows the path of one of Markov's chains.

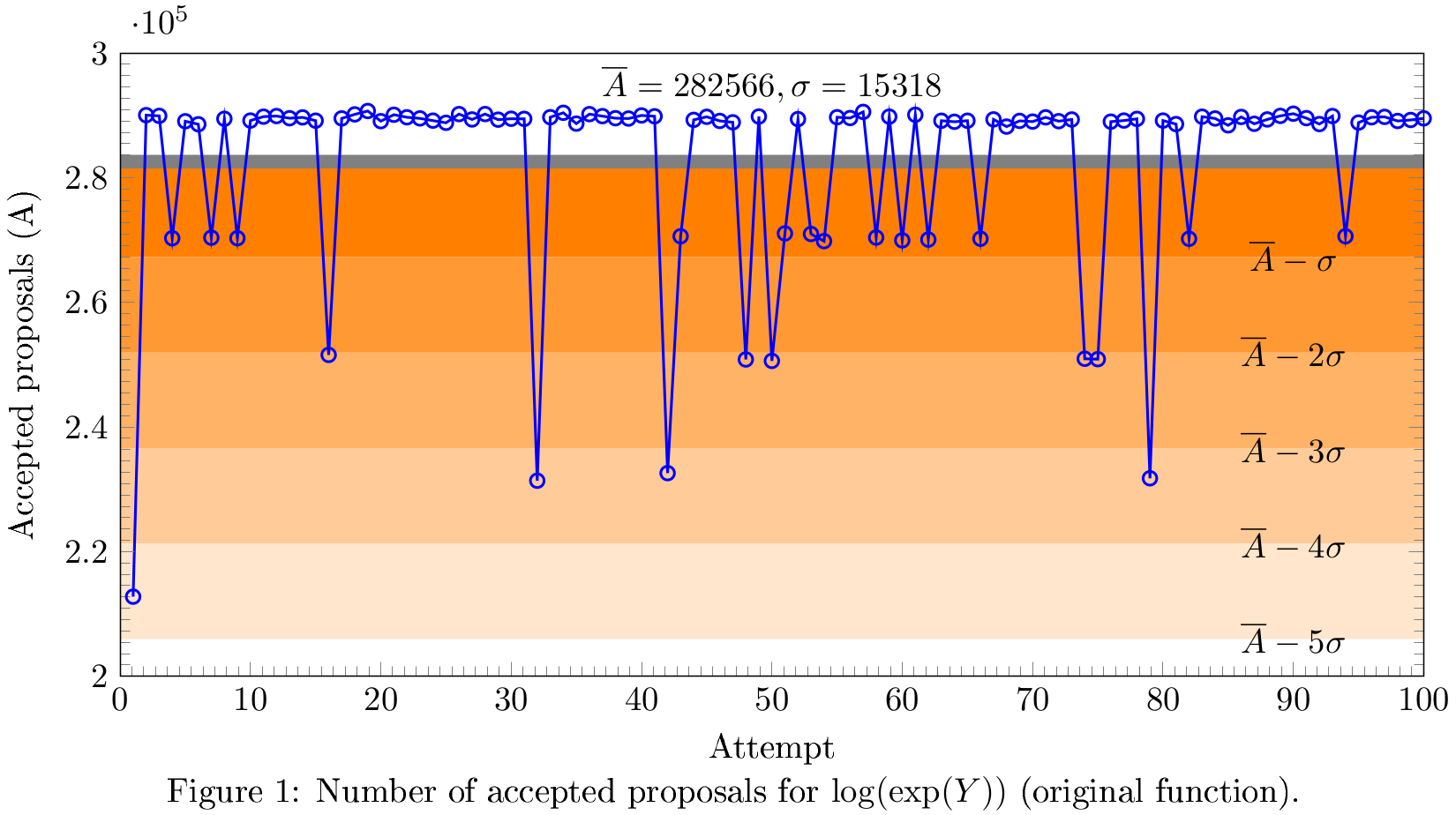
Когда я стал гонять код много раз, случайным образом начиная из разных точек, я решил посчитать количество одобренных решений о переходе в следующую комнату. Чисто логически, если мы 350000 раз (это количество независимых цепей опробования, умноженное на количество шагов расчёта - очень значимое число) бросим монетку, мы должны получить что-то около 175000 (на графике ниже - не монетка, но сути не меняется). И если мы в это сильно не попадаем, значит, что-то не так. То ли монетку протереть, то ли очки помыть.

I started to repeat code for many times, starting from different locations within the domain. I decided to print out number of accepted moves. If I drop a coin for 350000 times (that's number of sampling chains multiplied by steps, looks pretty enough), I expect it to show each side for ~175000 times (the plot below is not about the coin, but the logic remains the same). If I observe something far from it, it's a point to think about. May be I need to wash my glasses or I should clean the coin.

Видны лютые "провалы", некоторые из которых вылетают за три-сигма (то есть, с очень большой вероятностью, они не отражают истинного положения вещей). Среднее (серая линия) смещено относительно моды (самого частого значения).

One may see severe pitfalls out of three-sigma (so that they may not represent the function of interest). Average (gray line) is off the mode (the most probable value).

Что это значит? Это значит, что-то идёт не так. Оказалось, при уже не очень далеко ушедших параметрах (в уравнении функции) показатель степени уходит в -1000 и дальше. Экспонента принудительно приравнивается к нулю (в машинных терминах это называет underflow) - эти области по углам графика на первой картинке очерчены зелёным. Этот машинный ноль в старой модификации алгоритма прекрасно работал, а в новой от него брался логарифм. Тот на нуле обращается в бесконечность, которая, в свою очередь приводит к нечисленному значению (Not a Number). А оно, в свою очередь, приводит к тому, что какие-то цепочки вообще не начинают двигаться - и именно поэтому начинаются провалы в пиках. Кстати, то, что отклонение идёт ступеньками примерно по 20000 - это как раз 1-2-3-4 не заработавших цепочки.

What does it mean? Something goes wrong. I found that even slight offset of the parameters given to the function the power of the exponent goes to -1000, and the expression goes to zero (underflow, to be more correct) - these areas in the corners of the first plot are marked with green borders. In the older version of the algorithm (Multiple-Try Metropolis) it was fine. The newer code changed a bit, so that I had to take a logarithm before. Log returned infinity, which went to Not-a-Number. Finally, some of the chains were not able to move, causing pits in acceptance rates. This explains the stairs on plot: there are several steps by 20000 values. 

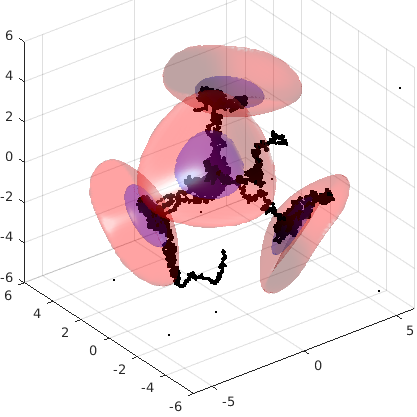
Видно, что пока часть цепочек исследуют все области интереса (фиолетовые), часть (чёрные "мухи") так и не сдвинулись с места. Напоминает меня в поисках пива. Если дают только пиво, то приходится ходить за дозаправкой, а вот если дать мне сразу смесь пива и абсента 50/50, то после первой же пары литров я никуда не пойду. Но цепям Маркова так нельзя! 

One may clearly see some chains are exploring all the regions of interest (violet), other (black spots) haven't moved even a bit. Resembles me a bit. If I have only beer, I need to hang around to get some more fuel again and again, while in case I started with few litres of beer and absinthe mixed 50/50, I won't move. But Markov chains should not be like me!

Проблема решилась просто: заменой конструкции "логарифм экспоненты" на само выражение. Математическая логика расчёта при этом пострадала, но это именно тот случай, когда компьютер накладывает ограничения на математику, а не наоборот. Когда я это исправил, всё заработало:

The issue was solved simply by conversion from log(exp(f(x,y,z))) to f(x,y,z) itself. That corrupted a bit the mathematical logic of the procedure, but computations prevail. After next trial, the plot converted to something nice:

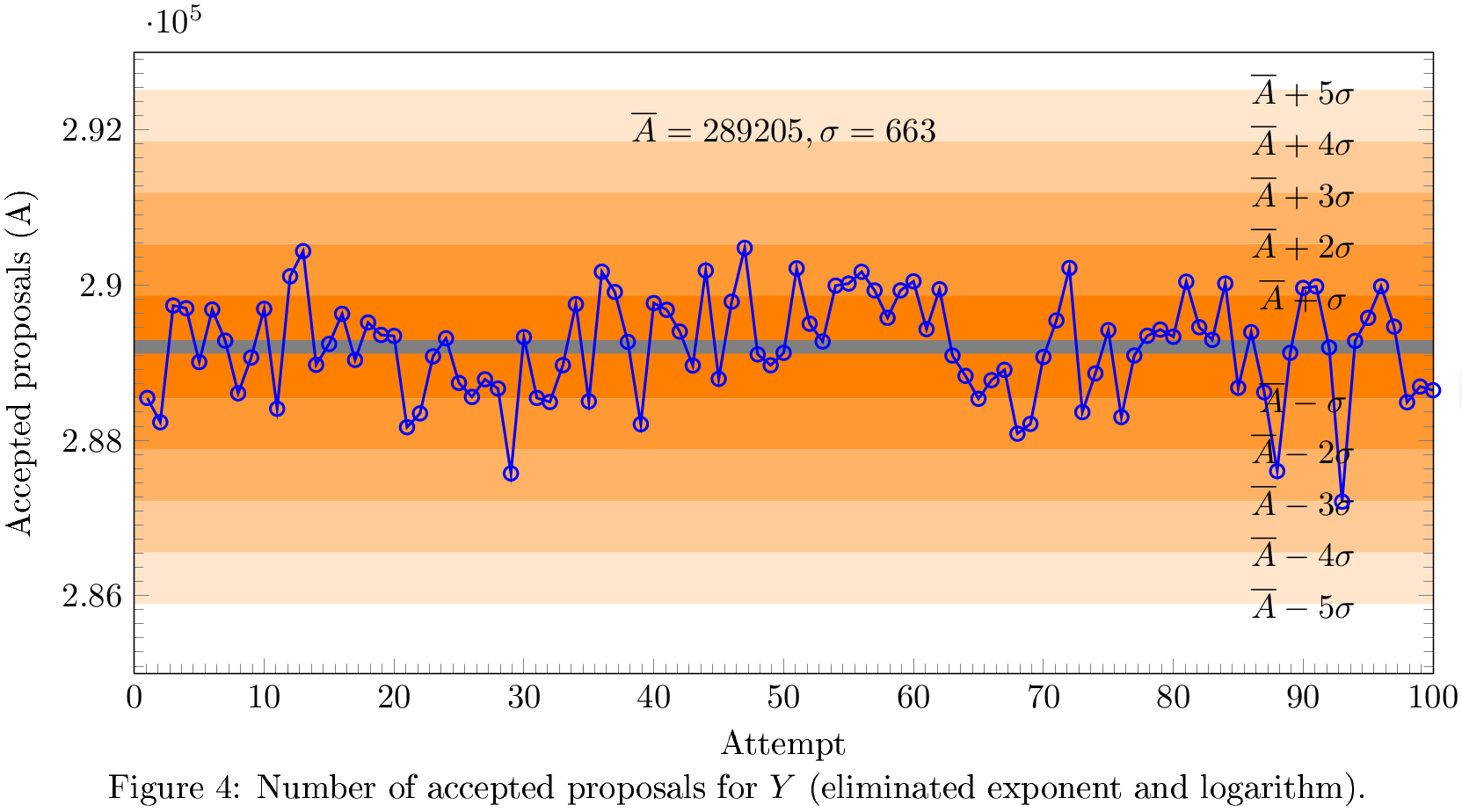
Мы видим равномерное (нормальное) распределение

A good normal distribution

В этот раз абсента никому не дали, и добавку приходится искать всем.
This time there was no absinthe, so that everybody have to look for next drink

Для меня это оказалось какой-то очень убедительной демонстрацией мощности (в статистическом и не только смысле) методов Монте-Карло. По сути, они автоматически дают базу для выявления корректности модели по внутренним характеристикам (то есть, без привлечения внешних данных). Это очень ценное качество, поскольку подогнать внешние данные можно какие угодно, а вот если сам метод показывает какие-то выбросы - где-то ошибка.

That was a very great demonstration to me how powerful are probabilistic Monte-Carlo methods. They give an option to check internal data consistency (i.e. without external data sources). That's a very important characteristic: one may find data to prove or reject a lot of statements, but here method itself tells something is wrong.