В природе нет чистых веществ. Все кристаллы, несмотря на то, что мы привыкли говорить "кристалльно чистый", содержат множество примесей других веществ. Иногда эти примеси заметны невооружённым взглядом, как например знаменитые зональные турмалины, иногда же их можно выявить только под микроскопом.
Турмалины (из коллекции Университета Лозанны)
Различные химические элементы, избирательно входившие в состав минерала на разных стадиях кристаллизации, окрашивали минерал в специфические цвета.
Под микроскопом становится видна зональность и плагиоклаза (серое зерно в центре кадра, образец с влк. Унзен, Япония).
Зональность кристаллов имеет важное значение для учёных, поскольку позволяет восстановить историю роста кристалла и историю той среды, в которой он рос.
Если мы берём любую "случайную" породу, то содержание в ней полезных для человека минералов и элементов, например, рудных, пренебрежимо мало. Для того, чтобы из породы получилась руда, природа должна для нас как-то собрать обычно рассеянные компоненты в одно место, откуда нам будет уже выгодно их извлекать. В том случае, если порода кристаллизуется из расплава, то запускаются процессы фракционирования (то есть избирательного обогащения каким-либо компонентом), приводящие к дифференциации (то есть изменению химического состава среды в каком-то направлении).
Лабораторным (но очень важным для промышленности) примером этого является зонная плавка - технология очистки вещества, основанная на многократном переплавлении вещества с образованием всё более и более чистого вещества.
Одним из предельных случаев такого процесса, по-видимому, являются магнетитовые вулканические лавовые потоки, содержащие миллионы тонн руд на железо, медь и золото (последнее - подчинённых количествах). Они известны в чилийских Андах ([Travisany et al., 1995] - в этой статье разобраны особенности пород, по которым авторы делают вывод о магматическом происхождении). Такие объекты известны и в других уголках планеты, например, в Китае ([Hou et al., 2011] - в этой статье приведена модель образования). Очень подробная статья на тему - [Williams, 2005]. Сначала в ходе кристаллизации магмы в магматической камере в остаточном расплаве накапливается железо. На каком-то этапе, как считается, происходит ликвация с отделением оксидного высокожелезистого расплава, который формирует свои собственные геологические тела. Целиком состоящие из руды, да.
Этот пример, думаю, достаточен, чтобы показать, что реконструирование эволюции химического состава среды может подсказать, где могут находиться залежи полезных ископаемых, а где их искать бесполезно. Да и, как получается, некоторые технологические процессы так или иначе скопированы у природы.
В этом посте я покажу, какими уравнениями описывается кристаллизация.
Прежде чем перейти к математическому описанию, надо ввести несколько величин.
Одним из самых распространённых в природе случаев, когда один элемент может замещать другой элемент - это магний и железо. Известно немало минералов (оливин, пироксены, амфиболы), где соотношение может меняться непрерывно от 100% магния до 100% железа. Для обозначения количества железа (или магния) используется мольная доля x(Fe) (или x(Mg)), величина которой может меняться от 0 до 1. Причём
x(Fe) + x(Mg) = 1
На рисунках x(Fe) обозначено как #Fe (смысл тот же).
Для обозначения той фазы (твёрдая или жидкая), в которой находится компонент, я буду писать x(Fe:S) и x(Fe:L) соответственно.
Для того, чтобы шёл процесс изменения состава среды, один компонент должен охотнее входить в кристалл, чем другой. Для описания этого можно использовать совсем простую величину, коэффициент распределения:
D = x(Fe:S) / x(Fe:L)
С этим коэффициентом только одна проблема. Если мы попытаемся промоделировать фракционную кристаллизацию (как - написано ниже), мы получим рост концентраций до значений > 1. То есть у нас становится больше 100% содержания железа в расплаве и минерале, что, конечно, бред.
Чтобы избежать этого, надо использовать не удобную величину, а правильную. Правильной является константа равновесия обменной реакции (железом и магнием между твёрдой фазой и расплавом). Её можно записать в виде:
KD = ( x(Fe:S)/x(Mg:S) ) / ( x(Fe:L)/x(Mg:L) )
Или KD = ( x(Fe:S) / (1-x(Fe:S)) ) / ( x(Fe:L)/(1-x(Fe:L)) ) , откуда можно легко получить уравнение связи количества железа в расплаве и твёрдой фазе в каждый момент времени. Константа равновесия является почти постоянной величиной, в отличие от коэффициента распределения (который на самом деле меняется в зависимости от состава расплава), поэтому с ней проблемы типа 146% не возникнет.
Соответственно, величина KD определяется в экспериментах.
И, наконец, третья величина, которая нам нужна - это количество расплава в системе F в молярных долях. Соответственно, количество твёрдой фазы будет 1-F.
Соответственно, величина KD определяется в экспериментах.
И, наконец, третья величина, которая нам нужна - это количество расплава в системе F в молярных долях. Соответственно, количество твёрдой фазы будет 1-F.
Итак, у нас есть три возможных случая.
Первый - это полностью равновесная кристаллизация. Всё твёрдое вещество успевает поменять свой состав, чтобы быть в равновесии с оставшимся расплавом. Второй случай - полностью неравновесная (фракционная) кристаллизация, когда кристалл вообще не взаимодействует с расплавом. Третий случай - частично равновесная кристаллизация, когда есть некоторый слой кристалла, взаимодействующий с расплавом.
Равновесная кристаллизация.
Это самый простой случай, когда мы можем просто написать
F * x(Fe:L) + (1-F)* x(Fe:S) = A
где A - это состав системы. В том случае, если мы вычисляем итерационно (пошагово), то это состав системы на предыдущем шаге, который вычисляется по такой же точно формуле.
Выражая один из составов ( x(Fe:L) или x(Fe:S) ) через другой с помощью KD, мы можем рассчитать эволюцию состава системы.
Для расчёта я использовал запись уравнений для расчёта состояния системы на каждом шаге, исходя из её предыдущего состояния (что помечено через @(t) и @(t-1)):
сигма и пси - вспомогательные величины. Получаются такие вот графики:
Выражая один из составов ( x(Fe:L) или x(Fe:S) ) через другой с помощью KD, мы можем рассчитать эволюцию состава системы.
Для расчёта я использовал запись уравнений для расчёта состояния системы на каждом шаге, исходя из её предыдущего состояния (что помечено через @(t) и @(t-1)):
сигма и пси - вспомогательные величины. Получаются такие вот графики:
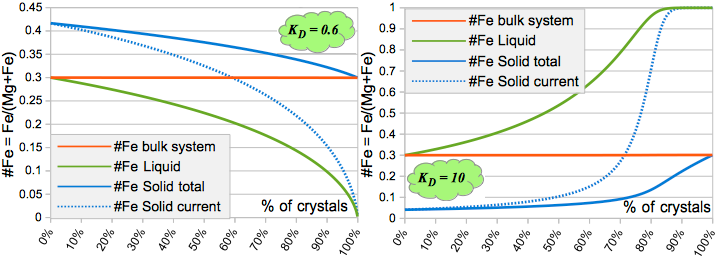
Равновесная кристаллизация при разных KD,.
В легенде обозначено текущее значение #Fe Solid (то есть то, что кристаллизовалось прямо на этом шаге). Так как кристаллизация равновесная, то оно совпадает с полным составом кристалла.
В легенде обозначено текущее значение #Fe Solid (то есть то, что кристаллизовалось прямо на этом шаге). Так как кристаллизация равновесная, то оно совпадает с полным составом кристалла.
В этом случае такой зональности, как на турмалинах на первой фотографии, образоваться не может. Состав кристалла является везде строго одинаковым.
Фракционная кристаллизация.
Зональность будет возникать в том случае, если кристалл не переуравновесился с внешней средой. Впервые уравнение эволюции состава расплава было получено Рэлеем (Rayleigh fractionation equation) в виде:
x(Fe:L) = x(Fe:L)0 FD-1
x(Fe:L)0 - начальное содержание элемента. Обращаю внимание на то, что здесь использован тот самый "неправильный" коэффициент распределения D, который приводит к неправильным значениям на высоких степенях фракционирования. Вывод уравнения подробно (и понятно) разобран в [Арискин, Бармина, 2000], и останавливаться на нём я не буду.
Если записывать правильным образом через KD, получаются такие уравнения (для схемы с последовательным вычислением):

Вот такие получаются графики, если предположить, что ширина зоны - 5% системы. Это несколько отличается от того, что мы видели в чисто фракционном случае.
Возможные ошибки
В системах уравнений последнее уравнение было названо уравнением контрольной проверки. Это уравнение проверяет, что ваш расчёт на каждом шаге не теряет и не производит вещество. В принципе, системы можно довольно сильно упростить, если это уравнение использовать в расчёте, допустим, валового состава твёрдой фазы из состава расплава (а не честным расчётом из состава твёрдой фазы на предыдущем шаге). Но тогда велика опасность пропустить ошибки в других уравнениях.
В качестве примеров графики, которые получались у меня из-за попыток так схитрить:
Если записывать правильным образом через KD, получаются такие уравнения (для схемы с последовательным вычислением):


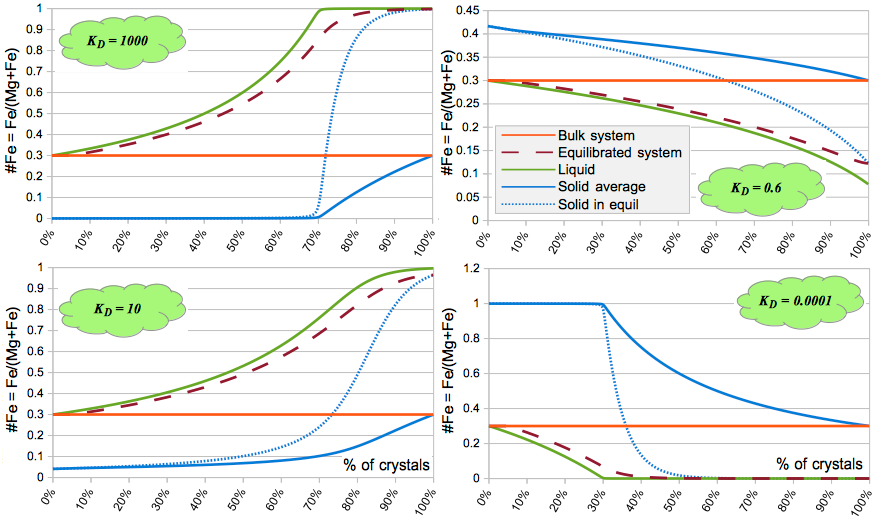
Вот здесь уже получается гораздо более интересная картина.
Средний состав сильно отличается от состава на данном шаге, что приводит к значительной эволюции состава расплава и твёрдой фазы.
Соответственно, если в какой-то момент, допустим, "отжать" жидкость, то можно получить, как на правом рисунке, чисто "железный" расплав, который даст железную руду, как в примерах выше.
В природе же у нас никогда не бывает крайних случаев.
Поэтому фактически следует ожидать, что внешняя зона кристалла может переуравновешиваться с расплавом. Здесь я написал уравнения из предположения, что Ф% от общего объёма системы - это пограничный слой кристалла. Если у нас кристаллов меньше, то действуют законы равновесной кристаллизации.
Сложность заключается в том, что состав системы и её количество меняются на каждом шаге.
Система уравнений:
Вот такие получаются графики, если предположить, что ширина зоны - 5% системы. Это несколько отличается от того, что мы видели в чисто фракционном случае.
Возможные ошибки
В системах уравнений последнее уравнение было названо уравнением контрольной проверки. Это уравнение проверяет, что ваш расчёт на каждом шаге не теряет и не производит вещество. В принципе, системы можно довольно сильно упростить, если это уравнение использовать в расчёте, допустим, валового состава твёрдой фазы из состава расплава (а не честным расчётом из состава твёрдой фазы на предыдущем шаге). Но тогда велика опасность пропустить ошибки в других уравнениях.
В качестве примеров графики, которые получались у меня из-за попыток так схитрить:
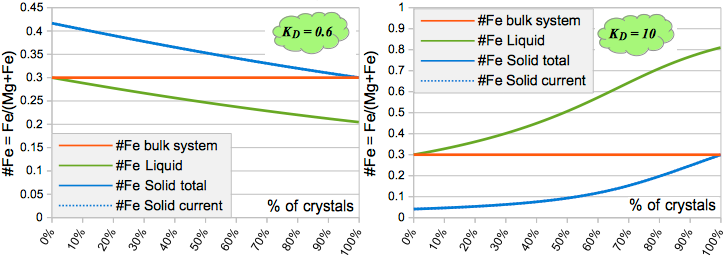
Конечно, очень хочется сказать, что промоделирована т.н. осциляционная зональность, но это не так. Это просто ошибка в уравнении.
И ещё один пример с потерей вещества.



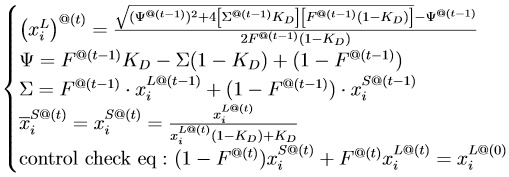



Комментариев нет:
Отправить комментарий