В этот раз расскажу немного о своей работе.
Передо мной была поставлена задача написать программу, которая бы моделировала плавление вещества в условиях нижней мантии Земли - это от ~660 до ~2900 км от поверхности Земли прямо вниз.
Прежде всего, надо где-нибудь подсмотреть, что там вообще творится. Один из наиболее свежих обзоров - это [Kaminsky, 2012] (здесь и далее я использую изображения-миниатюры с сайтов журналов, за полными версиями идите на сайт или пишите мне):
Сообразно картинке, в нижней мантии мы имеем в качестве главных минералов перовскит (а точнее, пироксен со структурой перовскита) (Mg,Fe)SiO3 (с некоторым количеством кальциевой разновидности) и периклаз (Mg,Fe)O.
Для того, чтобы понимать, что происходит в нижней мантии (а точнее - есть ли там расплав, который, по сейсмическим данным и учёным теориям, местами быть должен), нужна диаграмма плавления. Вот с этим уже хуже. По сути, есть только одна работа [de Koker et al., 2013], которая её приводит для сильно упрощённой системы из двух компонентов - SiO2 и MgO с добавкой третьего (FeO):
Есть три соединения, которые не образуют твёрдых растворов между собой - MgO, MgSiO3 и SiO2. Между ними образуются эвтектики. На рисунке показаны кривые для двух давлений (верхняя - для 136 ГПа, граница мантия-ядро, нижняя - 24 ГПа, граница верхней и нижней мантий). Разными цветами показаны разные количества железа.
Теперь кратко о том, что такое диаграмма с эвтектикой. Если у нас есть два химически несмешивающих в твёрдом состоянии вещества, то температура плавления смеси будет ниже, чем температура плавления каждого из них. Простейший пример - соль, которую бросают на улицы, чтобы растопить снег. Температура плавления воды 0 градусов, поваренной соли около 800 градусов, а вот их смесь тает уже при нескольких градусах ниже нуля. Нарисовать это можно таким образом (картинка с dic.academic.ru):
Ниже эвтектической изотермы у нас есть смесь двух твёрдых веществ. Выше кривых плавления - только расплав. Между солидусом (прямой) и ликвидусом (кривые) - зона, где есть и твёрдая фаза, и расплав (также как в воде может оставаться либо соль, либо снег). При повышении давления все линии будут смещаться вверх (в область более высоких температур, экзотические случаи обратного поведения мы здесь рассматривать не будем).
При этом состав жидкой фазы определяется кривой ликвидуса, а твёрдых - крайними линиями.
Любой состав системы описывается точкой на оси составов. Фазовый состав же может быть определён как сумма определённых количеств веществ, ближайших к этой точке, если смотреть по оси абсцисс.
Это уже можно пытаться промоделировать.
Часть 0. Зачем делать что-то самим?
Казалось бы, всё есть. Зачем городить что-то новое? Проблема в том, что построенная выше диаграмма потребовала очень много часов (дней ...) расчёта на весьма мощном компьютере. Это расчёт из первых принципов, ab initio, т.е. идущий из квантово-механических законов. Если мы хотим использовать её в своих расчётах, нам надо придумать что-то гораздо более простое. Описать всё простыми уравнениями и считать уже по ним.
Уравнения можно было бы предложить гораздо проще, чем предлагается тут, но. Если мы хотим сделать термодинамически согласованную (т.е. без потерь и появлений тепла из ниоткуда) модель - нужно пройти много боли и унижения.
Несколько подробнее Вы можете посмотреть обо всей этой кухне в моей презентации.
Несколько подробнее Вы можете посмотреть обо всей этой кухне в моей презентации.
Часть 1. Фазовая диаграмма плавкости при постоянном давлении
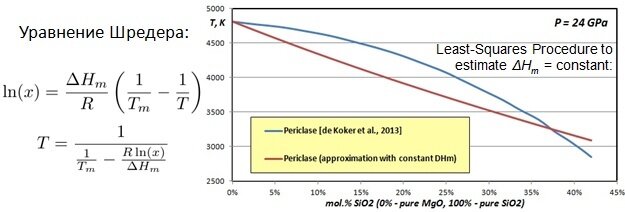
Главная задача - придумать уравнение, которое описывало бы поверхность ликвидуса. Теория предлагает уравнение Шредера. Однако наивные мечты на лёгкую жизнь обречены на провал. Из-за того, что расплав не является идеальным раствором, мы получим вот такую картинку:
То есть вместо синей линии мы получаем коричневую, которая ошибается градусов этак на 500.
Как ни странно, поверхности ликвидусов из статьи великолепно описываются параболами:
T = px^2 + qx + r
Часть 2. Подготовка к построению диаграммы плавкости для интервала давлений
В статье предлагается два крайних варианта - 24 и 136 ГПа. Но если мы будем пытаться промоделировать мантию, нам нужно будет получить и промежуточные давления.
Самым простым, а потому неправильным, будет попытка предположить прямую линию для интерполяции.
Правильным является использование уравнения Клаузиуса-Клапейрона, которое может быть записано как:
dp/dT = ΔH / (TΔV),
где слева производная давления по температуре, а справа - энтальпия фазового перехода (плавления) в числителе и произведение температуры на объёмный эффект реакции в знаменателе.
В приложениях к статье [de Koker et al., 2013] есть красивые картинки, которые показывают зависимости энтальпии (точнее, величины, из которой она может быть рассчитана) и объёма веществ от температуры и давления. С них посредством замечательной программки PlotDigitizer можно снять значения.
Для использования в программе можно брать "классические" уравнения типа [Birch, Murnaghan, 1947], [Holand, Powell, 1998] и другие. Их минусы в том, что они содержат много коэффициентов, крайне неудобны для расчётов (если их надо проводить ОЧЕНЬ много раз, точнее, миллионы) и вообще хочется чего-то более наглядного.
Потому я взял и написал такие простые формулы:
V = (aT + b)P^2 + (cT +d)P + (eT+f)
H = (zT + y)V^2 + (xT +w)V + (vT+u) + PV
Несмотря на радикальную простоту, уравнения описывают приведённые авторами значения с точностью в пределах 2%, в паре случаев - 5%, что более чем прекрасно (и едва ли не лучше, чем уравнение [Birch, Murnaghan, 1947]).
Для получения коэффициентов при постоянной температуре я сначала использовал ОЧЕНЬ приятное on-line приложении Polynomial Regression Data Fit.
Потом я решил "хватит это терпеть" и написал простенькую систему уравнений, которая получала сразу все 6 коэффициентов для каждой из величин методом наименьших квадратов.
Потом я решил "хватит это терпеть" и написал простенькую систему уравнений, которая получала сразу все 6 коэффициентов для каждой из величин методом наименьших квадратов.
Теперь вопрос, что делать с этим добром. Как гласит мануал [Жариков, 2005] (кстати, в нём можно прочитать очень много всего интересного "про это"), “В двухкомпонентной системе уравнение Клаузиуса-Клапейрона будет описывать трёхфазовую моновариантную реакцию”, что в переводе с русского на понятный означает, что уравнение может быть применено только для чистых фаз и для точки эвтектики (где пересекаются кривые).
Для двух точек для каждой кривой ликвидуса мы можем провести простейшую итерационную процедуру:
T = T + Δp / (dT/dp)
Итерационность проистекает из нелинейности. Искать аналитическое решение мне было лениво, а расчёт таким методом одной кривой из другой даёт результат в пределах погрешностей самих кривых (что было очень приятной неожиданностью).
Вот что получается в итоге для одной из эвтектик:
Правда, няшненько? ;)
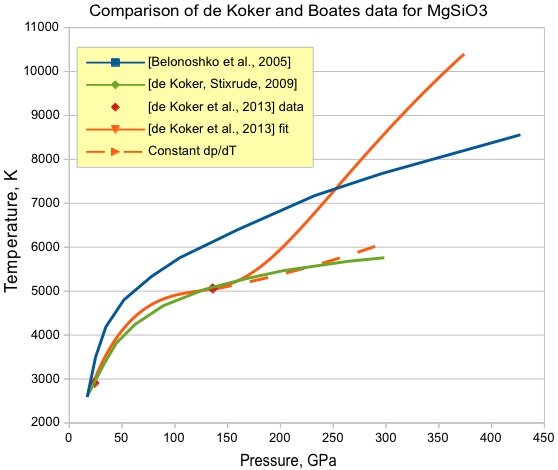
То, чем мы занимались выше, называется извра интерполяцией: мы находились между точками, для которых авторы статьи приводят данные. Если же мы попробуем уравнения экстраполировать в область высоких давлений, получим следующее (для примера взят MgSiO3):
Эта картинка великолепно демонстрирует, насколько всё относительно. Синенькая линия - расчёт ab initio (как и в используемой статье), но выполненный 8 лет назад с другими допущениями.
Красные точки - это данные из статьи [de Koker et al., 2013]. Зелёная линия - это расчёт этого же коллектива несколькими годами ранее (они согласуются! Ура!!). Рыжая линия - это если пытаться всё считать по приведённым выше уравнениям. В интервале 24-136 ГПа всё отлично, а вот с 170 ГПа начинается какая-то лажа - она уходит резко вверх.
Можно поступить весьма просто: просто объявить при всех давлениях выше 136 ГПа градиент постоянным (пунктирная линия). В общем, работает очень неплохо - в пределах погрешностей расчётов!
Часть 3. Построение диаграммы плавкости для интервала давлений.
Как было сказано выше, мы можем посчитать значения температур для отличных от реперных давлений только для двух точек (эвтектики и чистого вещества). Но для описания ликвидусов мы используем параболы, в которых есть три коэффициента! Т.е. надо ещё одно уравнение.
Чтобы его найти, вспомним тот факт, что чистое вещество имеет максимум температуры плавления! Тогда всё просто! Коэффициент r - это температура плавления чистого вещества!
Что делать с p и q? Как я понял из курса Ландау-Лифшица, всякий раз, когда ничего не понятно, продифференцируй это! Продифференцировав параболу, получим:
Что делать с p и q? Как я понял из курса Ландау-Лифшица, всякий раз, когда ничего не понятно, продифференцируй это! Продифференцировав параболу, получим:
T' = 2px + q
Подставив граничные условия на симметрию парабол (и помня, что в левой части магическим образом получается разница температур плавления чистого вещества и эвтектики), легко получаем из исходного уравнения выражения, которые позволяют пересчитать параболу для любого давления!
Можно сделать проще - например, зафиксировать p. Но в таком случае наши вершины наших парабол начнут смещаться. Фактически это приведёт к тому, что мы начнём сильно врать с составом и температурой ликвидусной жидкости.
PS: в случае твёрдых растворов, мы можем пользоваться и обобщённой формой уравнения Клаузиуса-Клапейрона, см. [Walker et al., 1988]. Но в случае несмешивающихся фаз оно не имеет смысла.
Итак, мы сделали половину работы!
Мы можем построить диаграмму плавкости для любого давления!
PS: программная реализация этого потребовала всего-то ~600 строчек программного кода и около 100 констант для расчётов.
Часть 4. Подготовка к плавлению и кристаллизации
Сначала надо будет написать функции, которые (1) возвращают температуру солидуса/ликвидуса для данного химического состава (давление здесь и далее предполагается заданным), (2) по температуре возвращают равновесный состав жидкости в зависимости от состава системы (учитывая то, какую твёрдую фазу мы имеем) и (3) для данной температуры по валовому химическому составу системы возвращают фазовый состав (количество и состав жидкости и твёрдых фаз) в системе. Третья функция в точках эвтектик и плавления чистых фаз не определена.
Рассчитывать правильно теплоты плавления/кристаллизации крайне важно, так как они в разы выше теплоёмкостей веществ! Фактически это может привести к искажению температуры твёрдого вещества после кристаллизации в десятки градусов!
Следует отметить, что тут везде повествование идёт для простой картинки с одной эвтектикой. На самом деле, практически все функции содержат цикл, чтобы выбрать одну из двух половинок исходной диаграммы.
Случаи чистых фаз, которые плавятся без эвтектик, для удобства рассчитываются в программе отдельно от эвтектик.
Рассчитывать правильно теплоты плавления/кристаллизации крайне важно, так как они в разы выше теплоёмкостей веществ! Фактически это может привести к искажению температуры твёрдого вещества после кристаллизации в десятки градусов!
Следует отметить, что тут везде повествование идёт для простой картинки с одной эвтектикой. На самом деле, практически все функции содержат цикл, чтобы выбрать одну из двух половинок исходной диаграммы.
Случаи чистых фаз, которые плавятся без эвтектик, для удобства рассчитываются в программе отдельно от эвтектик.
Часть 4. Плавление!
Вводные данные: количество теплоты, которое мы сообщаем системе, стартовая температура. Для простоты рассматриваем нагрев от полностью твёрдого состояния.
Часть 4a. Субсолидусный нагрев (только твёрдые фазы)
Тут всё просто. Рассматриваются два случая. Либо тепла дано с избытком, и мы греем до температуры солидуса, либо греем только до величины тепло/(теплоёмкость системы).
Часть 4b. Эвтектика
Тут надо немного поломать голову, вникнуть в особенности барицентрических координат и написать несколько уравнений, которые будут описывать изменения в количествах твёрдых фаз и увязывать с количеством эвтектического расплава.
Опять же, рассматриваются два случая: теплоты дано с избытком, или её не хватает.
В первом случае мы просто образуем требуемое количество расплава.
Во втором - количество расплава равно теплота/(удельная теплота плавления).
Часть 4c. Расплав + твёрдая фаза
Здесь нельзя посчитать также просто, так как теплота плавления нелинейно зависит от температуры. Оптимальным оказалось рассчитывать температурный шаг в зависимости от разницы температур ликвидуса и солидуса (ΔT/40). В том же случае, если тепла не хватает на выполнение шага по температуре, шаг по температуре делится на два, затем - ещё раз, и так, пока количество неучтённой теплоты ни станет пренебережимо мало (например, 1 Дж/моль; для сравнения, для того, чтобы нагреть 1 моль воды на 1 градус, нужно 75.6 Дж энергии).
В статье приведены данные по термодинамическим параметрам только для отдельных составов. Расчёты показали, что в центральной части диаграммы теплоты плавления различаются довольно мало (от 0 до ~15%, что в пределах точности расчётов), поэтому была использована линейная интерполяция значений для промежуточных составов.
В статье приведены данные по термодинамическим параметрам только для отдельных составов. Расчёты показали, что в центральной части диаграммы теплоты плавления различаются довольно мало (от 0 до ~15%, что в пределах точности расчётов), поэтому была использована линейная интерполяция значений для промежуточных составов.
Часть 4d. Расплав
Финальная температура рассчитывается как отношение количества оставшегося тепла к теплоёмкости.
Часть 5. Кристаллизация!
Вводные данные: количество теплоты, которое мы должны отнять у системы, стартовая температура. Для простоты рассматриваем охлаждение от полностью жидкого состояния.
Часть 5a. Охлаждение расплава
Тут
всё просто. Рассматриваются два случая. Либо тепло забираем с избытком, и
мы охлаждаем до температуры ликвидуса, либо охлаждаем только до величины
тепло/(теплоёмкость системы).
Часть 5b. Расплав + твёрдая фаза
Здесь считаем почти также, как в 4c, за искючением одного нюанса. Нам нельзя считать тут эвтектику! Здесь легко допустить ошибку, когда мы в следующий блок будем передавать полностью закристаллизованную систему!
Часть 5c. Эвтектика
Часть 5d. Расплав
Тут всё аналогично пункту 4a, только в обратную сторону.
Часть 6. Технические детали
Время расчётов для большинства тестовых случаев составило 3 миллисекунды, включая вывод на экран и в файл.
Погрешность расчётов (разница начальной заданной температуры и конечной, если мы сообщаем и забираем одинаковые количества тепла), не превышает нескольких десятых долей градуса и является машинной точностью расчётов (т.е. может быть увеличена при соответствующем росте времени расчёта).
Правда, чтобы добиться этого, потребовалось несколько дней и полкило интуиции (чтобы угадывать, где надо чинить, а где уже машинная точность начинается).
Часть 7. Третьи компоненты.
В том случае, если у нас появляется ещё один компонент в небольшиз количествах (как, например, железо), то температуры ликвидусов содержащих его фаз будут снижаться. В первом приближении это снижение можно считать линейным (от количества железа).
В таком случае мы можем просто перед началом всего расчёта снизить температуры эвтектик (и подвинуть сами эвтектики по горизонтальной оси!) и ликвидусов на определённую величину.
Ура! Всего лишь 1100 строк кода и 111 основных констант
- и наша модель работает!




Комментариев нет:
Отправить комментарий