Как зависит размер учебника от его названия?

Думаю, многие замечали, что "краткий курс" какого-нибудь предмета занимает меньше места, чем название курса без каких-либо приставок. Я решил провести небольшое исследование, чтобы понять, насколько этот феномен оправдан.

В качестве тестового предмета был выбран математический анализ. Этот предмет, в отличие от многих других, читается почти всем естественно-научным специальностям и является базовым для практически всех остальных разделов математики. Поэтому логично предположить, что для этого предмета будет довольно много учебников, написанных разными авторскими коллективами и разными научными школами.

Была составлена выборка из 53 изданий XX-XXI века, изданных в СНГ или СССР. Эти учебники представляют собой базовый курс в том или ином виде. Задачники не входили в список.

Итак, результаты:

 

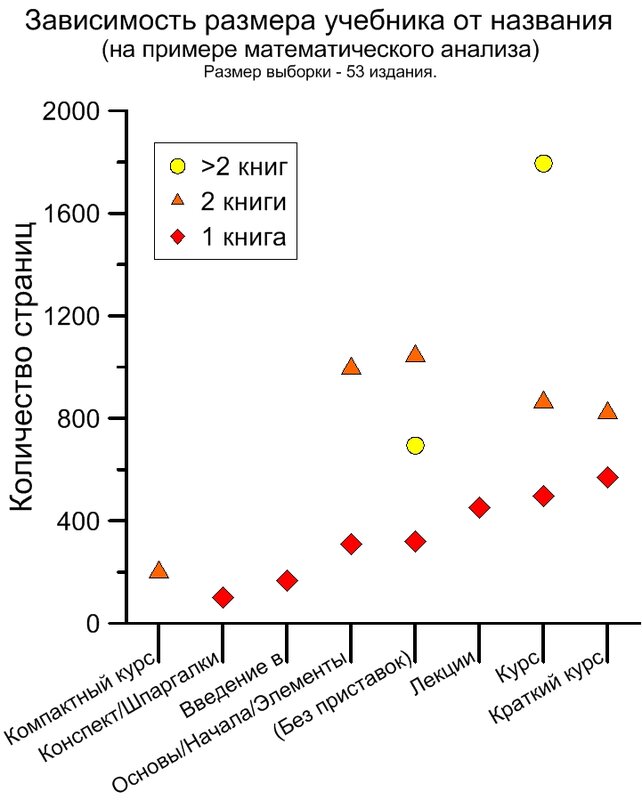
Сразу стоит отметить точку "Компактного курса". Есть только одно издание с таким названием, которое было выделено отдельно. Как Вы видите, слово "компактный" математик понимает совсем по-другому, чем слово "краткий". Эту точку следует исключить из дальнейшего рассмотрения, так как в этом случае математик пользуется для определения размера курса термином, который строго определён в самой математике.

Что касается однотомных изданий, наблюдается довольно забавное увеличение их размера, причём самыми толстыми оказываются учебники, названные "краткими курсами". Их размер в два раза больше, чем "Основ математических анализов" или "Математических анализов".

"Введения в математический анализ" оказываются очень тонкими. Они получают 167 страниц в среднем только благодаря учебнику Шахмейстера в 792 страницы. Без него их средний размер менее 89 страниц (что даже меньше среднего конспекта). (За этот абзац спасибо Станиславу Иванову).

Двухтомные издания демонстрируют строго обратную картину: из размер уменьшается от "просто" "математических анализов" к "кратким курсам".

Многотомные издания называются либо "курс математического анализа", либо "математический анализ". Размер их довольно вариабелен: от 579 до 1852 страниц. При этом, ввиду авторской скромности, средний размер "курса" оказывается в два раза больше размера книги без приставок к названию.

Данная статистика не учитывает вариаций шрифта, полей и размера страниц, но академические издания обычно печатаются довольно схожими.

Успешного Вам выбора книги по математического анализу! И да поможет Вам статистика!

Буду благодарен за дополнения!

Список обработанной литературы:

1. Акилов Г.П., Дятлов В.Н. Основы математического анализа. 1980, 338 с.
2. Аксенов А.П. Математический анализ. 2004, 614+759 с. 
3. Архипов Г.И., Садовничий В.А., Чубариков В.Н. Лекции по математическому анализу. 2004, 640 с.   
4. Бермант А.Ф. Курс математического анализа. 1959, 467+358 с.
5. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. 2005, 736 с. 
6. Берс Л. Математический анализ. 1975, 520+544 с.
7. Виленкин Н.Я., Мордкович А.Г. Математический анализ. Введение в анализ. 1983, 191 с. 
8. Виленкин Н.Я., Куницкая Е.С., Мордкович А.Г. Математический анализ. (--). 1978-1979, 161+177 с.
9. Воронина Б.Б. Математический анализ. Конспект лекций. 2007, 160 с.
10. Гимаев Р.Г. Введение в математический анализ и дифференциальное исчисление функции. 1997, 72 с.
11. Гурова З.И, Каролинская С.Н, Осипова А.П. Математический анализ. Начальный курс с примерами и задачами. 2002, 352 с.
12. Гурса Э. Курс математического анализа. 1933-1934, 368+235+271+287+276+320 с.
13. Дороговцев А.Я. Математический анализ. Краткий курс в современном изложении. 2004, 560 с.
14. Дьедонне Ж. Основы современного анализа. 1964, 430 с.
15. Зорич В.А. Математический анализ. 2002, 664+794 c.
16. Зубова И.К., Острая О.В. Введение в математический анализ. 2006, 117 с.
17. Иванов А.Б., Морева М.Б. Введение в математический анализ (--). 2008, 57 с.
18. Ивашев-Мусатов О.С. Начала математического анализа. 2009, 256 с.
19. Ильин В.А., Позняк Э.Г. Основы математического анализа. 2005, 648+464 с. 
20. Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ. 1985-1987, 662+358 с.
21. Казимиров Н.И. Математический анализ. Конспект лекций для первого курса. 2002, 92 с.
22. Карташев А.П., Рождественский Б.Л. Математический анализ. 2007, 448 с. 
23. Клевчихин Ю.А. Введение в математический анализ. 2002, 107 с.
24. Кудрявцев Л.Д. Краткий курс математического анализа. 2005, 400+424 с.
25. Кудрявцев Л.Д. Курс математического анализа. 2003-2006, 704+720+351 с. 
26. Кустов Ю.А., Юмагулов М.Г. Математика. Основы математического анализа: теория, примеры, задачи. 1998, 272 с.
27. Ландау Э. Основы анализа. 1947, 184 с.
28. Лесняк Л.И., Зголич М.В. Введение в математический анализ. 2008, 76 с.
29. Лобкова Н.И. Математика. Выпуск 2. Введение в математический анализ. Дифференциальное исчисление функции одной переменной. Опорный конспект. 2001, 132 с.
30. Ляшко И.И., Боярчук А.К., Гай Я.Г., Головач Г.П. Математический анализ (--). 2001-2003, 360+224+224 с.
31. Малугин В.А. Высшая математика. Основы математического анализа. 2006, 224 с.
32. Михаль Ю.О. Математический анализ. Шпаргалка для студента. 2007, 48 с.
33. Насыров С.Р. Введение в математический анализ (--).  2008, 88 с.
34. Немыцкий В., Слудская М., Черкасов А. Курс математического анализа. 1940-1944, 458+404 с.
35. Никольский С.М. Курс математического анализа. 1983, 464+448 с.
36. Никольский С.М. Курс математического анализа. 2001, 592 с.
37. Ногин В.Д. Введение в математический анализ. 1994, 62 с.
38. Решетняк Ю. Г.  Курс математического анализа. 1999-2001, 454+512+442+444.
39. Романовский П.И. Общий курс математического анализа в сжатом изложении. 1962, 332 с.
40. Рудин У. Основы математического анализа. 1976, 320 с.
41. Свиридюк Г.А. и др. Математический анализ. 2000, 165+63+168+183 с.
42. Тер-Крикоров А.М., Шабунин М.И. Курс математического анализа. 2001, 672 с.
43. Толстов Г.П. Элементы математического анализа. 1974, 521+473 с.
44. Хавин В.П. Основы математического анализа. Дифференциальное и интегральное исчисление функций одной вещественной переменной. 1998, 448 с.
45. Хинчин А.Я. Восемь лекций по математическому анализу. 1948, 261 с. 
46. Хинчин A.Я. Краткий курс математического анализа. 1957, 628 с.
47. Фихтенгольц Г.М. Основы математического анализа. 1968, 422+464 с. 
48. Франклин Ф. Математический анализ. 1950, 336+344 с.
49. Шахмейстер А.Х. Введение в математический анализ. 2009, 792 с.
50. Шварц Л. Анализ. 1972, 838+534 с.
51. Шведов И.А. Компактный курс математического анализа. 2003, 113+88 с.
52. Шилов Г.Е. Математический анализ. 1972, 528+517 с.
53. Эрмит Ш. Курс анализа. 1936, 384 с.