Атомное моделирование

Краткое содержание предыдущих серий (чем я занимаюсь и как это получается): я занимаюсь созданием термодинамически-согласованной модели плавления вещества в нижней мантии Земли (это между 660 и 2900 км вглубь нашего шарика). Для этого мною взята из литературы единственная существующая на данный момент база результатов расчётов температур плавления и некоторых термодинамических величин [de Koker et al., 2013],  по которой я пишу программный модуль, чтобы для для заданных температуры, давления и состава породы рассчитать, какое вещество там находится (твёрдое или жидкое) и какие у него свойства.

Умные люди сначала посмотрят, насколько правдоподобна модель (описание свойств веществ), и будут решать, нужна ли она им. К сожалению, такой путь нам заказан по двум причинам. Во-первых, модель нужна, а другого нет всё равно, а что-то лучше, чем ничего. Во-вторых, единственная годная статья написана настолько феноменально удобно, что предоставляет только некоторые параметры (удельный объём и внутренняя энергия) только в виде графиков. Нам же нужны (для сравнения с альтернативными источниками информации) теплоёмкость, коэффициент термического расширения, температуры плавления  и прочие параметры, которые в статье вообще не приводятся. Таким образом, в любом случае сначала необходимо пересчитать все данные в те величины, которые уже можно сравнивать с другими данными.

Программный же блок в любом случае потребуется. Описанная в прошлой статье его навороченная архитектура призвана обеспечить в первую очередь лёгкую заменяемость табличных констант, по которым рассчитываются все величины. То есть есть блок констант, который может быть легко изменён. Есть блок функций с параметрическими функциями (т.е. не следующей напрямую из теории, а удобный для расчёта полином) базовых термодинамических параметров от констант. Опять же, функции легко заменяются независимо друг от друга. И есть блок совсем внешних функций, расчёты в которых основаны на термодинамических соотношениях и которые используют параметрические функции. То есть любой кусок куда может быть изменён или дописан, и (1) любой параметр вычисляется только в одном месте, то есть не надо вычищать его расчёт в куче мест и (2) изменения коснутся сразу всех зависимых функций и ошибок не будет.

Теперь посмотрим, что же получилось. Начнём с приятного.

Напомню кратко суть модели. [de Koker et al., 2013] сделали компьютерное моделирование структуры ряда веществ (твёрдых и жидких), которые должны быть в нижней мантии Земли. Такого рода моделирование содержит немало допущений и неточностей, которые будут рассмотрены ниже, и которые делают необходимой постоянную сверку результатов с данными, полученными по другим моделям.

Термодинамические параметры - согласованость с другими значениями.

Теплоёмкость. Синее - то, что используется сейчас. Красное - предсказанное по альтернативной модели (perplex - единственный, по сути, софт, который может дать хоть какие-то предсказания значений величин, исходя из твблиц термодинамических свойств). Зелёное - по указанной выше статье. Сходимость в пределах 10% - это очень и очень неплохо. С теплоёмкостью я возился, кстати, долго. Из-за сочетания кривизны моих рук и общего скудоумия в течение месяца я рассчитывал теплоёмкость в полтора раза больше реального значения, что доставляло боль и унижение.

А вот так выглядит график для плотностей. Perplex - это альтернативная модель, PREM - общепринятая простейшая модель. Отклонения в пределах 2% - это успех.

График несколько отличается от приведённого в предыдущей статье, так как здесь использован профиль для мантийной адиабаты (специальным образом заданная температура).

Для сравнения с предыдущим графиком: 660 км - 24 ГПа, 2900 км - 140 ГПа (шкала нелинейная).

Коэффициент термического расширения тоже вполне приятный. Согласованный.

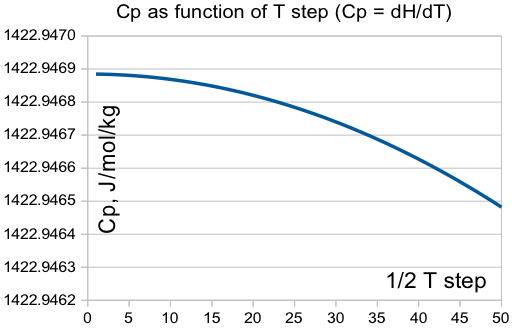
Важным параметром является устойчивость решений. В частности, теплоёмкость определяется на производная энтальпии по температуре Cp = dH/dT. Очень приятно было убедиться, что она не зависит от шага по температуре:

Температура плавления.

С ней всё значительно хуже. Для примера рассмотрим простое чистое вещество MgO, которого в нижней мантии должно быть процентов 20 от состава.

Вот так выглядит неполная сводка графиков зависимости температуры плавления MgO от давления. Весь верхний пучок - это расчёты на компьютерах. Две жалкие ниточки в середине - это экспериментальные данные (да, очень мало экспериментов!). Чуть больше данных для FeO. Жирная чёрная линия - это температурный профиль для мантии (мантийная адиабата). Ступенька соответствует границе мантия-ядро.

Почему с температурой плавления всё плохо?

Для этого надо немного копнуть в сам метод моделирования. Это Molecular Dynamics. Великолепная презентация по методу лежит тут, к которой я и отсылаю заинтересованного читателя. Если совсем кратко, то суть метода такова. Создадим несколько сотен виртуальных атомов. Для начала опишем их простейшей ньютоновской физикой, а потом будем довешивать всякие бонусы для более реалистичного описания свойств атомов. Запустим при давлении и температуре в расчётную ячейку. Подождём. Посмотрим, что получится.

Метод очень популярен не только в геологии, но и в физике, и в биологии (по биологии - половина материалов), и в наноматериаловедении.

Что удивляет - нет методических работ. Есть куча работ с расчётами для конкретных веществ, но очень мало работ, в которых бы обсуждались погрешности и ограничения метода. Интересующие вещи приходится выковыривать из совершенно левых работ - других просто нет.

Вторая проблема в том, что в статьях вообще не приводится конкретики. Пишется "мы посчитали методом Molecular Dynamics". Это примерно как если аллергик спросит в ресторане, из чего приготовлено блюдо, а ему скажут "всё съедобно". Есть множество методических приёмов и прочих "фишек", которые вообще остаются за кадром. Соответственно, весьма сложно и понять, о чём идёт речь.

Теперь немного теории. Плавление - это не одномоментный процесс. Это не щёлкнул пальцами - оно стало жидким. Процесс очень сильно зависит от скорости поступления тепла и прочего. Желающие могут поэкспериментировать со снегом. Для того, чтобы кристаллическая структура перестала существовать, все атомы должны "уйти" со своих позиций. И наоборот, чтобы застыла жидкость, должны образоваться зародыши кристалликов, которые постепенно вырастут и займут собой весь объём.

А вот теплоёмкость, удельный объём и прочие параметры от передвижений атомов зависят очень слабо.

Иллюстрация раз.

График из статьи [Sankaranarayanan et al., 2006]

Ступенька по вертикальной оси соответствует переходу жидкость (вверху) - твёрдое (внизу).

При нагреве фазовый переход происходит при на 400 (!) градусов большей температуре, чем при остывании.

Справедливости ради, надо отметить, что как минимум частично эффект соответствует действительности: кристаллизация начинается при переохлаждении относительно равновесной температуры, а плавление - при перегреве. 

Для того, чтобы избежать этого, были предложены различные методики. 

В частности, [Belonoshko, 1998] предложил элегантное решение проблемы: а давайте мы в расчётную ячейку сразу запустим расплав и кристалл? Кто кого пожрёт, тот и молодец!

На графике для двух веществ (разными цветами) пунктиром показаны расчёты по классической схеме, а сплошными линиями - по предложенный методике. Точки - экспериментальные данные. Комментарии излишни.

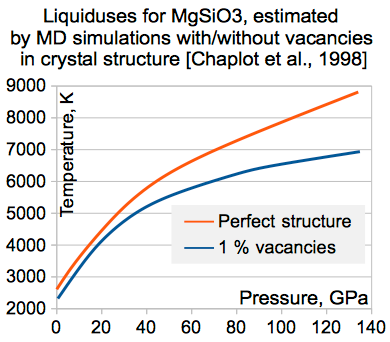
А вот это - ещё один интересный эффект. Если в кристалле оставить 1% вакансий (т.е. просто без атомов), температура плавления снижается процентов на 10-15, причём данный эффект вполне реалистичен. А в природе идеальных кристаллов нет. 

Почему с температурой плавления всё ещё хуже, чем показано выше?

В литературе описаны чисто и численные эффекты.

Количество атомов N, участвующих в расчёте, влияет на температуру плавления!

Количество кристаллической фазы напрямую зависит от длительности времени, в течение которого "жила" структура виртуальных атомов [Yamamoto, 2005].

Для сравнения, в [de Koker et al., 2013] моделирование не превышало 1 наносекунды (это время в моделировании, расчёт, понятно, занимает гораздо больше реального времени). Такие же времена фигурируют и в других статья. Систематических исследований нет.

Чем делать?

Таким образом, предполагается, что читатель на этой стадии уже схватился за голову и пошёл нервно курить. В общем, это верное решение. 

Тем не менее, работать как-то надо. Самое простое решение: это взять из модели [de Koker et al., 2013] всю термодинамику, которая, как показано в первой части, работает, а температуры взять из экспериментов.

Для этого как раз можно обратиться к диаграмме, приведённой выше, и аналогичным для других нижнемантийных минералов.

Это позволит пересчитать для чистых минералов (здесь - для MgO) температуры плавления.

Вопрос в том, что делать с более сложными составами. 

Здесь сразу встречный вопрос: а какие составы мы хотим учитывать? У нас есть чуточка вещества из верхней мантии и нет никакого вообще вещества из нижней мантии (не считая нескольких крохотных включений в алмазах, см. мою заметку). Единственное, на что мы реально опираемся - это данные расчётов, исходя из химического состава Солнечной системы (одна из самых популярных статей на тему - [McDonough, Sun, 1995]). 

На поверку оказывается, что есть пара главных компонентов (MgO, SiO₂), которые слагают процентов 80 породы. А остальные - это резко второстепенные в количестве до 10%. Это позволяет посидеть с бумажкой и за минут 10 написать что-то в духе (формула выведена с безумным количеством допущений и работать не должна):
\[ \Delta T = - \frac{RT^2\gamma}{\Delta H_m - \int_{T_m}^{T_m} C_p dT} K_D x_b^S \]

Эта формула содержит две величины, коэффициент распределения K_D и коэффициент активности гамма, которые индивидуальны для каждого вещества. Мы их не знаем. Общепринятое решение в петрологии на этот случай - написать просто:
\[ \Delta T = \alpha \Delta x_b^S \]

где альфа - это эмпирическая константа. Несмотря на переупрощённость, эта формула в реальности работает весьма неплохо. Нелинейности альфа соизмеримы с погрешностями измерений температуры в экспериментах.

Для нас самой важной величиной является энтальпия плавления. Она относительно слабо зависит от примесей и может быть положена постоянной для заданных давления и температуры. 

Подборка экспериментальных данных.

Для того, чтобы набрать данных по альфам для каждого вещества, надо сделать подборку экспериментальных данных в духе:

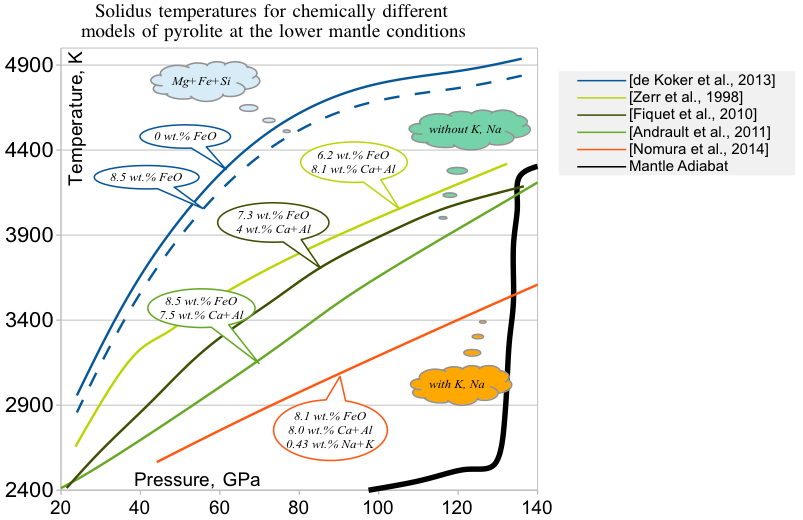
Эта диаграмма температура плавления - давление для состава нижней мантии позволяет установить, что Al и Ca не имеют значительного влияния на температуры плавления, так как не меняются сонаправленно с температурой. А для железа можно установить коэффициент порядка 100 К / 1 wt.% FeO. 

Na и K, несовместимые элементы, оказывают в разы более сильный эффект.

Выводы-заключение

(0) Очень мало данных. Очень мало хоть каких-либо систематических исследований, несмотря на попсовость и раскрученность всех упомянутых тем. Это действительно обескураживает, когда выбирать приходится между моделированием плавления металлов и протеинов (!), а оценить надо ошибки для оксидов.

(1) Численное моделирование позволяет получить весьма точные оценки для всех параметров, кроме температуры плавления.

(2) С температурой плавления всё сложно. Верить ей в общем случае нельзя. Она завышена на 10-20%.

(3) Можно ввести такие поправки, что температура плавления будет реалистичной, и все остальные параметры при этом не пострадают.

Наноприложение.

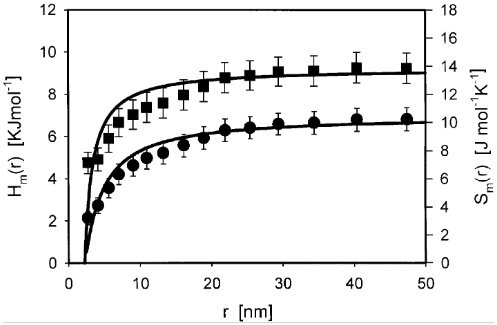
Новым для меня явилось то, что в наномире энтальпия и энтропия плавления зависят от размера частицы.

Энтальпия (сверху) и энтропия (снизу) плавления в зависимости от размера частицы [Zhang et al., 1999]