Плавление без проблем / Melting with no problems

Давно я не писал ни о каком о прогрессе по работе. Потому что его не было. Но вот мне удалось прорешать все основные проблемы, и таки оно заработало (об этом, надеюсь, в скором времени будет отдельный пост). А сейчас я опишу несколько проблем, с которыми мне пришлось столкнуться. Возможно, кому-нибудь поможет. Например, мне, если я снова в это упрусь.

Приношу извинения за то, что текст весьма тяжёлый.

Once upon a time I was being writing smth about my work. However, that time has gone, but I'd like to resurrect it. After some pain I got the code working, and now I want to write about some problems, that I was faced with. May be once it will help somebody or even me. 

Sorry, but the text below should be hard to read and understand for unexperienced reader.

Итак, постановка задачи. Выполняется расчёт. Есть 2D дискретная сетка (может быть и 3D, здесь не суть важно), в которой сосуществуют твёрдая фаза и расплав с фазовыми переходами между ними. Они могут взаимно перемещаться (закон Дарси и адвекция/конвекция) и обмениваться химическими соединениями (химическое равновесие). Для этого и расплав, и твёрдая фаза представлены единичными "атомами", которые "плавают" по этой 2D сетке с течением времени. Время, что важно, дискретно.

Хим.состав и температура (при заданных граничных условиях) на каждом шаге усредняются для каждой ячейки исходя из этих "атомов".

Task in brief. There is a 2D (3D) numerical grid to perform calculations of advection/convection and Darcy flux for liquid and solid substances. Those substances have different chemical composition (which tends to equilibrate) and various proportions (they can melt/solidify). Those properties like temperature, mass, chemical composition etc are carried by tracers - numerical dots flowing in virtual space. So on, on each timestep each grid cell gets properties as an average of tracers within it.

Дискретность сетки №1 / Grid resolution issue #1

Итак. Цвета внизу - процент жидкости (чем краснее - тем жидче). Видны границы ячеек. Точечки - те самые "атомы": красные - жидкость, синее - твёрдая фаза. Видно, что при плавлении ячейки образуются новые "атомы", которые по закону Дарси текут вправо (сетка повёрнута на 90 градусов относительно вертикали). Дискретность сетки приводит к тому, что "капля" сразу по пересечении границы ячейки застывает. Естественно, это неправильно. Лечится использованием при усреднении свойств ячейки не просто среднего по "атомам", а средневзвешенного с учётом расстояний до центра ячейки.

Внимательный читатель может спросить: а почему, если в левых ячейках много расплава, они показаны синим? Связано это с проблемой визуализации. В этих ячейках расплав и твёрдая фаза оказались равны по плотности, поэтому они не разделяются, а красные точки расплава так и остались "сзади" синих точек твёрдой фазы. Да, проблемы визуализации - это та ещё головная боль.

So. Colors in the lower part of image shows percent of liquid in cells, and upper part represents tracer distribution in cells. We (at least, I) can see borders of cells, and dots are those traces. Melting produced new tracers, which go because of Darcy flux (note the grid is rotated perpendicular to the vertical axis). Discretization of space by grid causes effect of immediate solidification of the liquid drops as soon as they cross cell boundaries. This is caused because non-weighted averages of tracers were taken to get cells' properties. It is enough to cure it just to switch to distance-weighted averages.

You can find, that cells on the left part of image are filled by blue "solid" tracers, while they are shown to have a lot of melt. This is a bug of visualization. These cells contain melt, but it has the same density as the solid counterpart, so melt remains at the same position as it was formed. Rendering of image results that solid tracers overlap those of liquid. 

Дискретность сетки №2 / Grid resolution issue #2

На этом видео вы можете видеть образование "червячков" Арракиса. Их образование происходит в следующие стадии:

(1) вещество ячейки подогревается и плавится.

(2) образуется расплав с другой плотностью, который хочет утечь

(3) пока он течёт, программа сама "находит" эту капельку, и прибавляет новый расплав (который образовался по мере дальнейшего прогрева) к ней. Так сделано, в частности, чтобы снизить ресурсные потребности расчётов.

(4) но как только капелька расплава пересекает границу ячейки, программа о ней "забывает", и создаёт новую.

Проблему это создаёт как с точки зрения издержек памяти, так и некоторых дальнейших алгоритмических проблем, связанных с сильной неоднородностью (неслучайностью) распределения этих точек.  

Решение проблемы состоит в том, чтобы в ячейках проводить объединение капелек с сильным преимуществом (дополнительный весовой коэффициент) по оси Z (по которой идёт перемещение).

Here you can see The Birth of Worms:

(1) heating causes melting of cell's substance

(2) melting produces liquid with contrast density, which wants to separate from solid.

(3) while this melt remains within the cell, program finds automatically the closest molten tracer to add new-formed melt (if heating is going on) to it.

(4) as soon as tracer-droplet crosses the boundary, program "forgets" about it.

Problems are excess of memory required for extra tracers (computational costs) and some other issues, because algorithms used in our code pre-assume uniform and random tracer distribution rather than their spatial organization.

Solution is nearly simple: you can merge those droplets with high preference for Z-axis (direction of moving). It is performed adding an extra weight coefficient to distance formula.

Распределение теплогенерирующих элементов  (HPE)

Distribution of the heat-producing elements (HPE)

В горных породах содержатся радиоактивные элементы, которые при распаде выделяют тепло. При моделировании геодинамических процессов на больших временах это тепло может оказаться существенным.

Rocks contain radioactive elements, which decay produce heat. Long term processes like numerical simulation of global-scale geodynamics, should take it into account. 

На этой картинке смотрим на тёмно-синий и сиреневый графики. Видно, что второй даёт существенно меньший всплеск по максимальной температуре на сетке с течением времени (о нём - в следующем разделе).

This figure contains two plots. Dark blue has much higher maximum temperatures within computational domain than violet one.

Причина этого в разных описаниях разделения химических элементов. Геохимическая литература приводит два коэффициента - $D$ и $K_D$ ($X_{HPE}^L$ - содержание HPE элементов в расплаве, $X_{HPE}^S$ - содержание HPE элементов в твёрдой фазе):

Gap is caused by different approach to describe HPE partitioning. There are two main coefficients ($D$ and $K_D$) you can find in geochemical literature $X_{HPE}^L$ - concentration of HPE in liquid, and $X_{HPE}^S$ - their concentration in solid):

$D = \frac{X_{HPE}^L}{ X_{HPE}^S}$;   $K_D = \frac{X_{HPE}^L \cdot (1-X_{HPE}^S)}{ X_{HPE}^S \cdot (1-X_{HPE}^L)}$

$D$ - это то, что легко посчитать по экспериментальным данным: берёшь и делишь. Проблема в одном: на поверку он оказывается отнюдь не постоянным, и его величина зависит от количества расплава. Поэтому его использование (синий график) приводит, в конечном счёте, к делению на ноль и очень большом возрастании температуры). Не используйте $D$. Не пишите статей, где указываете $D$, но не указываете количества расплава. Будьте на стороне добра.

$K_D$ - это термодинамическая константа обменного равновесия. Она постоянна вне зависимости от количества расплава. Используйте $K_D$. Пишите про $K_D$. Она хорошая и добрая.

It's extremely easy to calculate $D$ from experimental data. But $D$ itself strongly depends on amount of liquid, so it cannot be assumed constant. Usage of it (and a constant as a value) causes division-by-zero, infinite amount of HPE and explodes the code (blue plot). Please, be cute and do not use $D$. Stay on the light side.

$K_D$ is a thermodynamic constant of exchange reaction, so it does not depend on actual quantity of liquid. It is just a constant. Use it. Like it. Be smart.

Сваливание в осцилляции

Falling down to oscillations

Плавление сопровождается поглощением теплоты, затвердевание - её выделением. В природе процессы идут недискретно (на макроуровне во всяком случае), потому если мы что-то плавим - это плавится, а если кристаллизуем - то застывает.

Когда мы пишем программный код, изменение температуры из-за скрытой теплоты (энтальпии) фазового перехода применяется только на следующем шаге. Получается, мы охладили ячейку - расплав застыл - выделилось тепло - кристаллы поплавились - скушали тепло - расплав застыл. Система сваливается в колебательный процесс. Этого, как показывают наблюдения, не бывает (редкие исключения - реакции типа Белоусова-Жаботинского). Это легко побороть, если ввести ограничения на количество вещества (в процентах системы, $dF$), которое может поменять своё фазовое состояние. Физический смысл этого - скорость протекания реакций.

Такой же эффект имеет изменение энтальпии плавления - но, конечно, в реальном мире мы так подкрутить не можем. К сожалению ;)

Melting consumes heat, and solidification produces it. Nature is designed so well, that we do not have discrete timesteps (at least, in geological timescale), and this processes go to the very end.

However, program code always use discrete timesteps, so our latent heat of fusion will be always applied next step from now. So such shit may happen: we cooled down a cell - melt froze - heat gets out - crystals melt - they ate the heat - melt froze. Such type of oscillatory process may take place in exotics like BZ reaction, but not in our primitive world of rocks. To deal with it, we can recall that all processes require some time - and limit $dF$, fraction of system that can change state on each timestep.

The same effect might be got by adjusting the latent heat itself. However we cannot cheat nature so easily :(

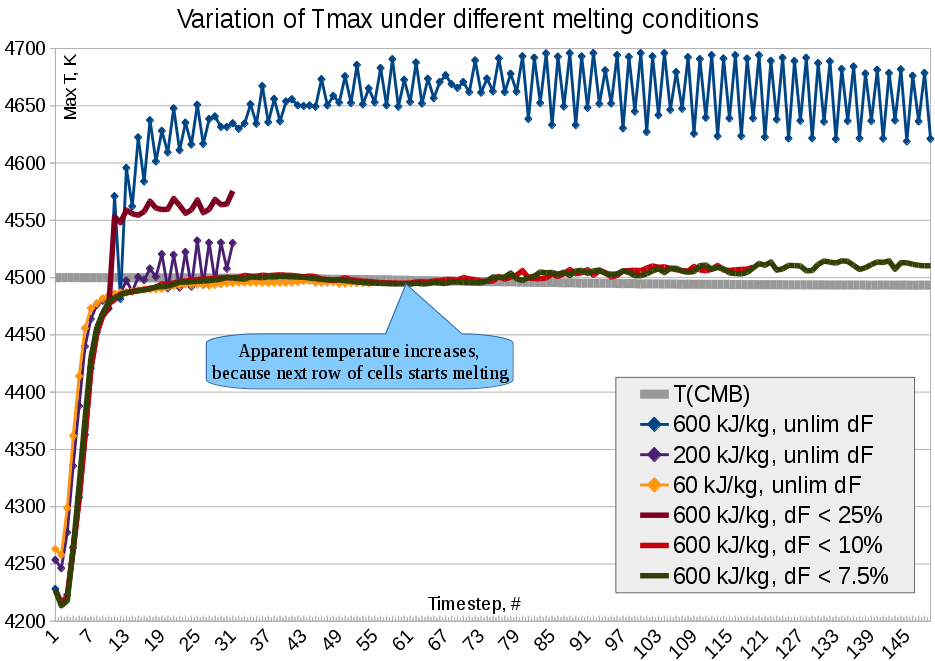
Можно увидеть, что некоторая пила, несмотря на все ухищрения, остаётся. И вот чтобы побороть её, надо ещё слегка подрихтовать функции плавления. Мы не должны полагаться на то, что она сама сойдётся к равновесному варианту, но мы должны определить температуру, при которой количество выделившегося тепла будет ровно таким, чтобы нагреть систему до точки равновесия. И двигаться к этой точке мы должны этими шажками с лимитированным $dF$.

However, some oscillations still remain. To cut off all of them we need to organize our melting routine in a way to predict exact amount of melt we do need to produce/solidify to fit be latent heat the equilibrium temperature. And we should move to it very accurately, so actually we converge both of $dF$ and temperature.

Нитевидный пульс на зелёном графике очень приятен. Температура никуда не уплывает. Остаточные пики вызваны фильтрацией расплавов: приток нового расплава меняет общий состав системы, и кажущаяся температура оказывается отличной от настоящей.

Thready pulse of the green plot is so cute!! Temperature oscillations are ceased. The rest is caused by melt filtration: new-came melt (by Darcy Flux) produces some additional heat.