Предисловие от автора блога
Иосиф Дементьевич Лукашевич (Józef Łukaszewicz) - геолог и революционер конца XIX - начала XX вв. Соучредитель террористической фракции партии "Народной воли" (не путать с самой "Народной волей"!), участник неудачной попытки убить Александра III, он был приговорён к смерти, но помилован. Этот геологический доклад в одной из высших научных организаций империи он прочитал через 2 (два!) года после выхода из заключения в Шлиссельбургской крепости, где он провёл 18 лет. Впоследствие он работал в геологическом комитете, а после революции 1917 года вернулся в родной город и стал профессором университета.
Я с огромным удовольствием прочитал текст его доклада. Прекрасный и ясный язык, огромное количество упомянутых исследователей со всего земного шара и широчайшая география наблюдений, использованных для подтверждения своей точки зрения. Очень надеюсь, что и читателям этот текст понравится не меньше.
Перед тем, как перейти к самому тексту, я хотел бы обратить внимание на некоторые моменты:
- "Разсчетъ показываетъ, что со времени возникновенія Альпійской системы протекло менѣе 20.000.000 лѣтъ." - по современным данным, Альпы начали формироваться 60 млн. лет назад и продолжают воздыматься сейчас. Оценка И.Д. превосходна с учётом имевшихся в его распоряжении данных - а первое радиоизотопное датирование было проведено в 1907 году, и, возможно, И.Д. даже не знал ещё об этой работе.
"ядро земли слагается изъ сильно сгущенныхъ газовъ, за нимъ слѣдуетъ толстый слой магмы, прикрытый снаружи твердой корой (...) считаю (...) наиболѣе вѣроятной" - доклад И.Д. состоялся за два года до открытия границы кора-мантия (поверхности Мохоровичича) и за три года до установления глубины раздела мантия-ядро. И.Д. крайне аккуратно интерпретирует имевшиеся на тот момент данные по температурам в недрах Земли (уже в конце XIX века было известно, что геотермический градиент возрастает с глубиной!) и по температурам плавления пород.
"опыты съ лавами Везувія и Этны показали, что для расплавленія застывшей лавы ее нужно нагрѣть на 50-100° выше той температуры, при которой она была еще въ жидкомъ состояніи". Лава всегда содержит воду и другие летучие компоненты, которые теряются при кристаллизации и которые снижают температуру плавления. Потому при попытке расплавить застывшую лаву её действительно нужно нагреть до более высокой температуры.
"Гауризанкаръ, высочайшую гору на землѣ" - процитирую вики: "гора в Гималаях на границе Китая и Непала (...). Название горы происходит от прозвищ индуистских богов Парвати и Шива. На рубеже XIX и XX вв. европейцы ошибочно именовали Гауризанкаром ещё более высокую гору, истинное название которой на тибетском — Джомолунгма. Гауришанкар является основой непальского времени и причиной необычного часового пояса (UTC+5:45)." - то есть И.Д. имел в виду именно Эверест!
Оцените! Конец XIX - начало XX века. Кто-то проводит точные геофизические измерения качения маятника на островах буквально по всему земному шару. И эти сведения доходят до Санкт-Петербурга и используются для оценки толщины земной коры! "Defforges находитъ, что на островахъ ускореніе тяжести вообще превосходитъ среднее значеніе, соотвѣтствующее данной широтѣ. На уединенныхь островахъ маятникъ, которымъ пользуются для измѣренія земныхъ ускореній, качается быстрѣе. На Бонинскихъ островахъ секундный маятникъ дѣлаетъ въ сутки 11,8 ударами больше, чѣмъ надо было бы ожидать, судя по георафическому положенію мѣста. На о. Уаланъ число лишнихъ ударовъ 8,7, на о. Св. Елены - 6,6, Ильдефрансѣ - 9,9, на Фернандо-Норонья - 9,4; на Шпицбергенѣ - 4,3. Наоборотъ, нигдѣ такого ускореннаго качанія маятника на берегахъ материковъ не замѣчается.". Сможете ли вы показать на карте Бонины, Кусаие (Уаланъ), о. Св. Елены, Маврикий (Ильдефрансъ), Фернанду-ди-Норонья, Шпицберген? С острова Уалан есть потрясающие литографии, прокрутите вниз страницы, там их много.
"Абсолютная глубина этой впадины отъ поверхности океана 9,6 килом" - опять же, в начале XX века такая точность оценки! Скорее всего, это результат немецкой экспедиции Вальдивия.
Текст подготовлен на основе сканированного изображения, которое я получил в Российской Национальной Библиотеке, и опубликован исключительно в научно-образовательных и культурных целях. Я постарался вычитать текст и найти ссылки на всех упомянутых учёных и неочевидные топонимы. Буду благодарен любым замечаниям! Приятного чтения!
Докладъ, читанный въ засѣданіи
Императорскаго Минералогическаго Общества
13-го Ноября 1907 года
Императорскаго Минералогическаго Общества
13-го Ноября 1907 года
Механика земной коры занимается изслѣдованіемъ общихъ условій равновѣсія матеральныхъ массъ на нашей планетѣ, массъ, слагающихъ горы и континенты. Такія огромныя скопленія вещества, какъ наша земля, вслѣдствіе мощнаго развитія въ нихъ молярныхъ силъ (1), обусловливаютъ своеобразныя явленія, которыя можно назвать планетарными процессами. При изученіи этихъ явленій приходится довольствоваться главнымъ образомъ наблюденіями и вычисленіями, такъ какъ экспериментъ въ отношеніи къ нимъ весьма мало примѣнимъ.
Вмѣшательство молярныхъ силъ, которыя внутри малыхъ тѣлъ совершенно незамѣтны, въ кругъ тѣхь физическихъ явленій, въ которыхъ участвуютъ огромныя массы вещества, дѣлаетъ то, что простыя аналогіи межъ малыми аггрегатами вещества и крупными теряютъ значеніе и даже просто становятся ошибочными. Пояснимъ это примѣрами. Вообразимъ два шара изъ чистаго желѣза: одинъ изъ нихъ діаметромъ въ 2 метра, другой діаметромъ равнымъ діаметру земли. Отличаются они только величиной. Оба они имѣли температуру въ 50°, а затѣмъ были охлаждены на 50° или до нуля. Т.е. у нихъ отнято было столько тепла на каждый граммъ вещества, чтобы температура его понизилась на 50°. Что произойдетъ? Малый шаръ охладившись до нуля, нѣсколько уменьшится въ объемѣ, этимъ дѣло для него и кончится. Отнятіе такого же количества тепла на каждый граммъ вещества у большого шара вызоветъ охлажденіе не на 50°, а только на 21°, вслѣдствіе развитія тепла въ большомъ шарѣ при сокращеніи его въ объемѣ. Эффекть для обоихъ шаровъ получился иной только вслѣдствіе разницы въ ихъ размѣрахъ.
Для разрыва стальной проволоки въ 1 кв. миллим. сѣченія требуется приложить грузъ въ 70 килогр. Соотвѣтственно этому, чтобы разорвать стальную болванку или цилиндръ съ діаметромъ, равнымь діаметру земли, понадобится сила въ 8925·1018 килогр. Это есть сила необходимая для преодолѣнія молекулярныхъ силъ сцѣпленія стали. Для того же, чтобы разорвать земной шаръ по плоскости экватора на 2 полушарія, понадобится сила въ сто разъ большая, несмотря на то, что земной шаръ состоить изъ жидкости, облеченной тонкой твердой корой.
Такъ молярныя силы въ дѣлѣ сцѣпленія частицъ земного шара превосходятъ молекулярныя силы, и поэтому неудивительно, что въ нѣкоторыхъ отношеніяхъ земной шаръ реагируетъ, какъ очень твердое тѣло, хотя вещество его и не находится въ твердомъ состояніи.
Отсюда понятно огромное значеніе молярныхъ силъ въ опредѣленіи общей формы небесныхъ тѣлъ. Если бы Земля, Венера или Юпитеръ состояли изъ твердаго вещества и имѣли цилиндрическую, коническую, кубическую или иную угловатую форму, то эта форма была-бы неустойчивой для такого огромнаго скопленія вещества, какъ эти планеты. Взаимное тяготѣніе частицъ преодолѣло бы ихъ молекулярное сцѣпленіе; въ своемъ стремленіи къ центру притяженія онѣ бы измѣнили первичную форму въ шаровидную, при чемъ остались бы отъ первоначальной формы только небольшіе выступы и угловатости. Возможные размѣры этихъ выступовъ опредѣляются напряженіемъ тяжести на поверхности планеты: именно, они обратно пропорціональны ускоренію тяжести на планетѣ. На Лунѣ, которая по своей массѣ въ 80 разъ меньше земли и на которой ускореніе тяжести около 6 разъ меньше земного ускоренія, высочайшая гора превосходитъ Гауризанкаръ, высочайшую гору на землѣ. Если-бы солнце остыло, то горы на немъ были бы представлены низкими холмами, не выше 350-500 метровъ. Шаровидная форма небесныхъ тѣль не есть случайность: она обязана молярнымъ силамъ, а не молекулярнымъ, отъ которыхъ зависить шаровидная форма капель жидкости.
Итакъ въ опредѣленіи общей формы небесныхъ тѣлъ первенствующая роль выпадаетъ на долю молярныхъ силъ. На второмъ планѣ стоить центробѣжная сила, благодаря которой шаръ сплющивается въ элипсоидъ вращенія (сфероидъ). Наконець, третьестепенное мѣсто занимаютъ молекулярныя силы, благодаря которымъ существуютъ различныя неровности на поверхности планеты и нѣкоторое уклоненіе формы планеты оть правильнаго сфероида. Такъ форма нашей земли или геоидъ лишь незначительно отличается отъ сфероида. Максимальное уклоненіе геоида отъ сфероида не превосходитъ въ ту и другую сторону 0,2 килом. По Мессершмитту, въ Европѣ геоидъ нигдѣ не уклоняется болѣе, чѣмъ на 20 метровъ отъ идеальнаго сфероида, въ Азіи и Америкѣ не болѣе, чѣмъ на 50 метровъ; впадины на океанической поверхности, если только онѣ существуютъ, не превосходятъ 50 метровъ.
Чтобы ближе оцѣнить взаимоотношеніе силъ молярныхъ, молекулярныхъ и центробѣжной, необходимо исходить изъ опредѣленнаго взгляда на внутреннее строеніе земли. Какъ извѣстно, на этотъ счетъ высказывались всѣ возможныя гипотезы. Одни (Моръ, Фольгеръ, Дж. Дарвинъ, Томсонъ, Гопкинсъ) считаютъ, что земля совершенно отвердѣла и содержитъ внутри только большихъ или меньшихъ размѣровъ бассейны огненно-жидкой магмы. Другіе (Рейеръ) хотя и допускаютъ твердое состояніе для большей части барисферы, но приписываютъ это огромному давленію, которое препятствуетъ переходу тѣлъ изъ твердаго состоянія въ жидкое, несмотря на высокую температуру. Третьи (Лазо, Мушкетовъ) предполагаютъ, что земля состоитъ изъ твердаго ядра, твердой коры и слоя огненно-жидкой магмы, лежащей межъ ними. Четвертые (Делонэ, Генесси и др.) считаютъ нашу планету состоящей изъ огненно-жидкой массы и твердой наружной коры. Наконецъ, пятые (Цепперицъ, Арреніусъ, Гюнтеръ и др.) допускаютъ, что ядро земли слагается изъ сильно сгущенныхъ газовъ, за нимъ слѣдуетъ толстый слой магмы, прикрытый снаружи твердой корой. Такъ разнообразны взгляды на счетъ внутренняго состоянія земли! Но не всѣ они одинаково основательны. Не входя въ критику этихъ взглядовъ, я только укажу, почему считаю гипотезу Цепперица-Арреніуса наиболѣе вѣроятной.
Извѣстно, что съ глубиною повсюду на землѣ наростаетъ температура, приблизительно среднимъ числомъ 1°С на каждые 33 метра глубины. Слѣдовательно, внутреннія части земли теплѣе наружныхъ. А въ твердыхъ тѣлахъ, нагрѣтыхъ неодинаково въ разныхъ частяхъ, теплота не можетъ находиться въ устойчивомъ состояніи: она перетекаетъ отъ мѣстъ болѣе нагрѣтыхъ къ мѣстамъ болѣе холоднымъ. Вслѣдствіе этого въ земномъ шарѣ идетъ тепловой потокъ отъ центра кнаружи, и теплота излучается въ пространство. Земля охлаждается, а оть охлажденія сокращается въ объемѣ. Сокращеніе же въ объемѣ, вслѣдствіе превращенія части потенціальной энергіи земной системы самой по себѣ въ кинетическую, а затѣмъ въ тепловую, развиваетъ огромное количество тепла, именно при сокращеніи земного радіуса на 1 сантиметръ выдѣляется 84·1021 малыхъ калорій (2). Эта теплота прогрѣваетъ весь земной шаръ, а охлаждается онъ только снаружи. Поэтому по направленію отъ поверхности земли до самаго центра температура должна наростать. Если уже на разстояніи 1/64 земного радіуса господствуетъ температура въ 1500°, то въ центральныхъ частяхъ мы въ правѣ ожидать - встрѣтить много тысячъ градусовъ, т. е. такую температуру, которая навѣрное выше критической температуры кипѣнія всѣхъ извѣстныхъ намъ тѣлъ, а въ особенности металловъ. Слѣдовательно, въ высшей степени вѣроятно, что центральная часть нашей планеты состоитъ изъ сильно сгущенныхъ газовъ.
Въ пользу газовой теоріи есть и другія данныя. Именно, напряженность размыванія даетъ опредѣленныя указанія на газовое ядро земли. Съ перваго взгляда кажется, что абсолютно нѣтъ ничего общаго межъ газовымъ ядромъ и денудаціей. Въ дѣйствительности же геологическія явленія такъ переплетены межъ собою, что нерѣдко по однимъ мы можемъ судить о другихъ, повидимому, не имѣющихъ ничего общаго съ первыми.
Проточная вода уноситъ въ моря ежегодно 9,5 куб. килом. твердаго вещества по изслѣдованіямъ Э. Реклю, 16 куб. кил. по Лаппарану, около 10-11 куб. кил. по моимъ разсчетамъ. Ежегодно съ материковъ смывается очень тонкій слой среднимъ числомъ около 0,1 миллим. толщины. Врядъ ли нужно доказывать, что напряженность размыванія горъ значительнѣе размыванія низменностей. Въ горахъ и колебанія температуры рѣзче, и стремительные потоки увлекаютъ не только мелкую муть, но и крупныя гальки, и ледники проявляютъ свою разрушительную дѣятельность, и всякіе обвалы и оползни случаются легче тамъ, гдѣ скаты круче. Поэтому если мы примемъ напряженность размыванія горъ равной средней напряженности размыванія всей суши, то мы не преувеличимъ своихъ разсчетовъ, а скорѣе ихъ уменьшимъ. Принявши же эту напряженность = 0,1 миллим., мы приходимъ къ заключению, что существованіе всякой горной системы ограничено во времени. Если какое нибудь плато вздымается на 1 килом. надъ уровнемъ моря, то понадобится максимумъ 1000000 / 0,1 = 10000000 лѣтъ, чтобы смыть его до уровня моря; допуская восходящія движенія въ размываемомъ плато, мы должны соотвѣтственно увеличить эту цифру. Разсчетъ показываетъ, что со времени возникновенія Альпійской системы протекло менѣе 20.000.000 лѣтъ.
Поднятіе горной системы должно совершаться быстрѣе, чѣмъ идетъ размываніе, т. е. болѣе 0,1 мм. въ годъ: иначе размываніе не дало бы подняться горамъ. А мы знаемъ, что горныя цѣпи существуютъ еще долгое время послѣ того, какъ процессы горообразованія въ нихъ закончились.
Образованіе складокъ въ земной корѣ свидѣтельствуетъ объ уменьшеніи земной поверхности. Такъ при образованіи Альпъ земная поверхность уменьшилась приблизительно на 120000 кв. кил. Т.е. если расправить всѣ складки Альпійской системы, то получился бы избытокъ поверхности въ 120000 кв. кил. противъ площади 300000 кв. кил., занимаемой въ настоящее время Альпами. Отсюда легко вычислить, насколько уменьшился земной радіусъ при образованіи Альпійской системы
$4\pi(X^2-R^2) = 120000$ кв. кил.; откуда $X-R$ = 0,65 кил. ($R = 6371$ кил.) (3)
Такъ какъ въ третичный періодъ на ряду съ Альпами поднялись величайшія горныя системы какъ Анды, Скалистыя горы, Гималаи, Пиренеи, Карпаты и т. д., то сокращеніе земного радіуса для образованія всѣхъ этихъ горъ должно было достигнуть 15-16 килом. Это сокращеніе радіуса есть слѣдствіе охлажденія земного шара. Охлажденіе земли, главнымъ образомъ ея раскаленнаго ядра, совершается очень медленно. По моимъ разсчетамъ (я принималъ геотермическій потокъ за стаціонарный, геотермическій градіентъ = 33 метр. и среднюю теплопроводность земли равной теплопроводности гранита) оказывается, что для охлажденія земли на 1° требуется около 4 милліоновъ лѣть. Гергезель, исходя изъ иныхъ положеній, вычисляетъ, что для охлажденія земли на 1° требуется 2,4 милліона лѣтъ. Такъ какъ со времени поднятія горныхъ цѣпей третичнаго возраста протекло менѣе 20 мил. лѣть, то за этотъ промежутокъ времени земля могла охладиться не боле, какъ на 5-6°. А если при этомъ ея радіусъ сократился на 15-16 килом. или объемъ ея на 819·107 куб. кил., или на 1/133,2 первоначальнаго объема, то на 1° уменьшеніе объема было 1/666 или 150/100000, т. е. въ 32 раза больше коэффиціента расширенія желѣза или въ 50 разъ больше коэффиціента расширенія горныхъ породъ. Отсюда мы заключаемъ, что коэффиціентъ сжатія земли не вяжется съ гипотезой, будто земля совершенно твердое тѣло, напротивъ, этотъ коэффиціентъ указываетъ, что внутри земли находятся жидкости при критическихъ температурахъ и газы, которые обладаютъ высокимъ коэффиціентомъ расширенія.
Что касается псевдоригидной теоріи земного ядра, то для нашихъ цѣлей достаточно будетъ сказать о ней нѣсколько словъ. Barus (1893 г.) показалъ, что точка плавленія діабаза возрастаетъ на 0,025° съ увеличеніемъ давленія на 1 атмосферу. Фохтъ доказываетъ, что Barus преувеличилъ въ пять разъ цифру и что въ дѣйствительности возрастаніе всего 0,005° на 1 атм. Сверхъ того повышеніе температуры плавленія отъ давленія идетъ небезпредѣльно, а достигаетъ максимума, послѣ котораго оно падаетъ. У изслѣдованныхъ тѣлъ повышеніе точки плавленія отъ давленія лежитъ межъ 0,009° и 0,03° на 1 атм. Хотя для магмы намъ пока неизвѣстно это повышеніе точки плавленія, но на основаніи изслѣдованныхъ тѣлъ мы заключаемъ, что это повышеніе температуры наростаетъ въ земной корѣ въ 5-10 разъ медленнѣе, чѣмъ геотермическій градіентъ. Поэтому давленіе не можетъ воспрепятствовать переходу горныхъ породъ въ жидкое состояніе внутри земли; оно только дѣлаетъ земную кору болѣе толстой, повышая точку плавленія. Поэтому мы считаемъ, что подъ твердой корой залегаетъ жидкая магма. Что находится еще далѣе за слоемъ магмы – это для насъ пока неважно, хотя наиболѣе основательнымъ является взглядъ, что центральныя части нашей планеты заняты сгущенными газами.
Въ какомъ же отношеніи находится твердая оболочка къ жидкому ядру земли? Можетъ-ли молекулярное сцѣпленіе частицъ литосферы съ успѣхомъ выдерживать центральное притяженіе въ силу закона тяготѣнія? Какъ извѣстно, небольшіе шары, имѣющіе крѣпкую оболочку, подобно орѣху, могутъ прочно сохранять свою форму, хотя бы внутри ихъ была пустота. Можетъ ли имѣть мѣсто нѣчто подобное и въ отношеніи земного шара? Заключать отъ малыхъ шаровъ къ большимъ мы не въ правѣ, такъ какъ съ увеличеніемъ массы шара возрастаеть центральное притяженіе, вслѣдствіе чего отношеніе молекулярныхъ силъ, величина которыхъ остается неизмѣнной и въ большихъ и въ малыхъ тѣлахъ, къ молярнымъ, которыя, возрастаютъ съ массой, мѣняется. Поэтому, чтобы рѣшить вышепоставленный вопросъ, мы разберемъ слѣдующій случай. Вообразимъ, что подъ всей земной корой имѣется прочная, незыблемая опора, за исключеніемъ одного участка коры, изъ-подъ котораго удалена опора. Въ этомъ случаѣ вѣсь этого участка будетъ стремиться сколоть его, оторвать отъ окружающей массы и опустить вглубь, а молекулярныя силы сцѣпленія, дѣйствующія въ пограничной вертикальной плоскости - въ боковыхъ стѣнкахъ скалываемаго участка, будутъ стремиться удержать его въ его положеніи. Тутъ произойдетъ борьба двухъ силъ: силы сцѣпленія и силы тяжести. Результатъ будетъ зависѣть оть размѣровъ скалываемаго участка.
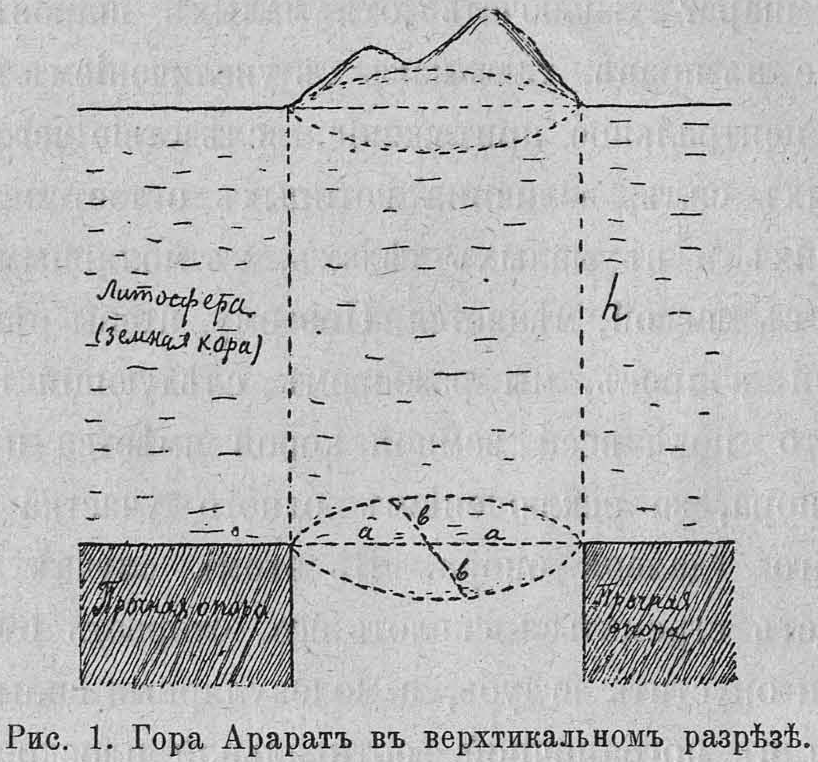
Сдѣлаемъ разсчетъ для Арарата. Эта гора, уединенно поднимающаяся на Армянскомъ плоскогорьи, занимаетъ своимъ основаніемъ эллиптическую площадь въ 85 кил. въ наибольшемъ и 25,5 кил. въ наименьшемъ діаметрѣ. Можетъ ли Арарать сохранить свое теперешнее положеніе въ силу сцѣпленія частицъ въ земной корѣ, если предположить, что магма удалена изъ-подъ того мѣста коры, надъ которымъ возвышается Араратъ, а вся остальная кора имѣетъ прочную опору.
Объемъ земной коры, находящейся подъ подошвой Арарата (рис. 1), будеть $\pi abh$, вѣсъ же ея $P = \pi abh \delta$ грамм. Боковая же поверхность эллиптическаго цилиндра будетъ равна длинѣ ($L$) дуги окружности эллипсиса, умноженной на высоту $h$, т. е. $Lh$. Обозначая черезъ $\phi$ сопротивленіе скалыванію 1 квадр. сант. поверхности (для базальтовъ $\phi$ = 285000 грам., для гранитовъ $\phi$ = 60000 грам.), получимъ общую величину молекулярныхъ силъ $F$, поддерживающихь эллиптическій вырѣзокъ земной коры, равной
$F = Lh \phi$
Отношеніе $P/F$ будетъ равно
$P/F=\frac{\pi abh \delta}{Lh\phi}=\frac{\pi ab \delta}{1,8\pi a \phi}=\frac{b \delta}{1,8\phi}=\frac{1275000\cdot 3}{1,8\cdot285000}=7,4$
Т. е. вѣсъ литосферы подъ Араратомъ въ 7,4 раза былъ бы больше, чѣмъ молекулярныя силы, поддерживающія этотъ вѣсъ въ горизонтальномъ положеніи, если бы въ этомъ мѣстѣ земная кора состояла изъ наиболѣе прочнаго матеріала - базальта. Если же предположить, что она состоитъ изъ гранита умѣренной прочности, то это будетъ гораздо ближе къ истинѣ, такъ какъ въ составъ коры входятъ породы и съ малымъ сцѣпленіемъ, да и съ глубиной, вслѣдствіе высокой температуры, сцѣпленіе понижается. Въ этомъ случаѣ отношеніе вѣса литосферы подъ Араратомъ къ молекулярнымь силамъ, противящимся скалыванію, будеть еще менѣе благопріятно, именно:
$P/F = \frac{1275000\cdot 2.5} {1.8\cdot 60000} = 29,5$
При этомъ мы еще не приняли во вниманіе вѣса самой горы, вздымающейся надъ плоскогорьемъ. Слѣдовательно только 1/30 вѣса земной коры, лежащей подъ Араратомъ, можетъ поддерживаться въ своемъ положеніи молекулярными силами, а 29/30 гидростатическимъ давленіемъ снизу. Если бы не было этого гидростатическаго давленія снизу, то Араратъ, несмотря на большую толщину земной коры, упалъ бы внизъ, пробивши въ земной корѣ отверстіе на подобіе того, какъ пуансономъ пробиваютъ дыры въ металлическихъ листахъ или пластинахъ.
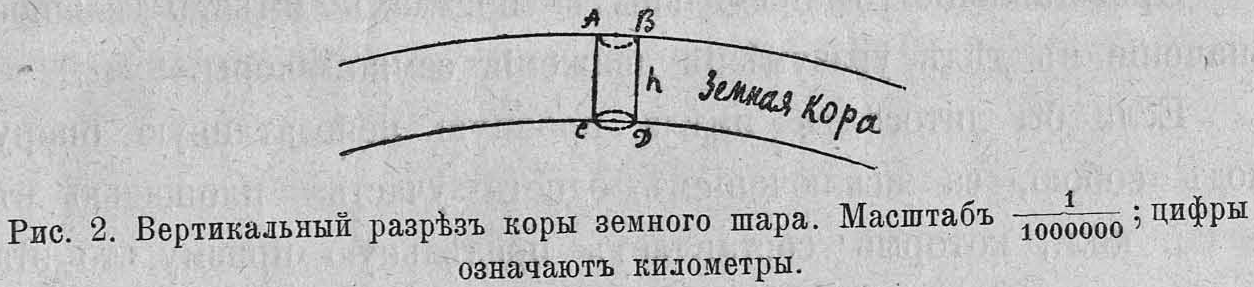
Теперь мы рѣшимъ вопросъ, какъ велика можетъ быть площадь земной коры, чтобы она еще могла удерживаться въ своемъ положеніи напряженіемъ молекулярныхъ силъ, т. е. разберемъ тотъ предѣльный случай, когда напряженіе молекулярныхъ силъ скалыванію или срѣзыванію равновелико вѣсу скалываемаго участка земной коры. Вообразимъ себѣ кругъ на земной поверхности съ радіусомъ $r$. Пусть толщина земной коры = $h$, средній удѣльный вѣсъ = $\delta$, сопротивленіе скалыванію $\phi$. Тогда вѣсъ цилиндрическаго вырѣзка изъ земной коры $ABCD$ (рис. 2), имѣющаго радіусъ = $r$, будеть $P=\pi r^2 h \delta$. Напряженіе молекулярных силъ поддерживающихъ этоть вырѣзокъ въ его нормальномъ положеніи будетъ $F=2\pi rh\phi$. По условію $P=F$; слѣд. $\pi r^2 h \delta =2\pi rh\phi$; откуда $r=2\phi / \delta$. Полагая земную кору состоящей изъ гранитовъ, будемъ имѣть $r = 2\cdot 60000 / 2,5=48000$ сант. $= 480$ метр. или діаметръ этого вырѣзка равенъ почти 1 километру. Округляя цифры, мы можемъ вообразить всю поверхность земного шара разбитой на 510 милліоновъ площадокъ, каждая въ 1 кв. кил. и сквозь контуры каждой площадки перпендикулярно къ ней проведемъ плоскости черезъ всю толщу коры. Тогда эта послѣдняя разобьется, подобно соту, на 510 милліоновъ равныхъ столбиковъ или призмъ, которыя будемъ называть предѣльными земными призмами.
Представленіе о предѣльныхъ призмахъ имѣетъ важное значеніе въ дѣлѣ уразумѣнія движеній земной коры.
Если бы литосфера имѣла прочную неподатливую опору подъ собою, за исключеніемъ одного участка площадью въ 1 кв. кил., который составляетъ предѣльную призму, то эта послѣдняя почти могла бы держаться въ своемъ положеніи напряженіемъ молекулярныхъ силъ, дѣйствующихъ въ ея стѣнкахъ и противящихся скалыванію или срѣзыванію. Если бы въ подобномъ положеніи очутились участки не въ 1 кв. кил., а въ 10, 500, 1000 и болѣе кв. кил., то уже молекулярныхъ силъ было бы недостаточно, и эти группы предѣльныхь призмъ стали бы осѣдать, опускаться внизъ, пока давленіе снизу не уравновѣсило бы ихъ избыточнаго вѣса надъ молекулярными силами. Напротивъ, участки менѣе 1 кв. кил. могутъ держаться въ свомъ положеніи сцѣпленіемъ частицъ литосферы, если земная кора, окружающая эти участки, имѣетъ прочную опору. Въ дѣйствительности, подъ корой залегаетъ огненножидкая магма. Поэтому всѣ предѣльныя призмы будутъ стремиться падать къ центру и въ этомъ своемъ стремленіи будутъ производить другъ на друга боковое давленіе. Такъ какъ предѣльныя призмы геометрически представляютъ собою усѣченныя пирамиды, мысленныя вершины которыхъ лежатъ въ центрѣ земли, то каждая предѣльная призма вставлена подобно пробкѣ или клину въ земную кору. Отсюда является вопросъ, быть можетъ это боковое давленіе, развиваемое призмами, или взаимное ихъ заклиниваніе можетъ воспрепятствовать паденію призмъ вглубь; быть можетъ, эти призмы, подобно замочному камню въ сводахъ, могутъ держаться напряженіемъ бокового давленія. Разсматривая каждую предѣльную призму, какъ клинъ, вставленный въ земную кору, мы легко можемъ вычислить то боковое давленіе, которое необходимо, чтобы преодолѣть вѣсъ призмы или клина. Вѣсъ предѣльной призмы $P=\pi r^2 h \delta$; алгебраическая сумма силъ, выталкивающихъ клинъ, вершинный уголъ котораго = $\alpha$, и уравновѣшивающихъ силу $P$ будетъ
$Z=\frac{P}{\sin(\alpha/2)} = \frac{\pi r^2 h \delta}{\sin(\alpha/2)}$
Такъ какъ боковая поверхность предѣльной призмы равна $2\pi rh$, то среднее напряженіе силъ на 1 кв. сант. боковой поверхности будетъ
$y=\frac{\pi r^2 h \delta}{\sin(\alpha/2) \cdot 2 \pi r h } = \frac{r\delta}{\sin(\alpha/2)}$
Для діаметра предѣльнаго цилиндра въ 1 километръ уголъ $\alpha=32"4$; поэтому
$y=\frac{r\delta}{\sin(\alpha/2)} = \frac{50000 \cdot 2,5}{0,000157} = 800000000$ грам. $= 800000$ килогр. на 1 кв. сант.
Если бы мы взяли діаметръ цилиндра въ 111 килом. (т. е. клинъ съ вершиннымъ угломъ въ 1°), то давленіе въ боковыхъ стѣнкахъ должно было бы равняться 795000 килогр. на 1 кв. сант. Давленіе же въ 800000 килогр. на 1 кв. сант. или почти 800000 атмосферъ столь чудовищно, что никакое твердое вещество не въ состояніи его выдержать: подъ такимъ давленіемъ всякое вещество придетъ въ совершенно текучее состояніе. Слѣдовательно, взаимное заклиниваніе предѣльныхъ призмъ никоимъ образомъ не можетъ задержать предѣльный цилиндръ или призму въ его стремленіи падать внизъ. Онъ можетъ развить такое давленіе, которое приведетъ стѣнки коры въ текучее состояніе; но еще раньше онъ можетъ раздвинуть стѣнки, заставивъ земную кору собраться въ складки, для чего не требуется особенно значительнаго бокового давленія. Такъ по изслѣдованіямъ Уиллиса и Хайеса для изгиба силурийскихъ известняковъ Аппалахской области достаточно было давленія въ 773-2390 килогр. на 1 кв. сант. Поэтому стѣнки коры не могутъ воспрепятствовать вертикальному движенію предѣльныхъ призмъ; онѣ только будутъ тормазить это движеніе.
Такъ какъ каждая призма состоитъ изъ цѣлаго ряда слоевъ, то давленіе верхнихъ слоевъ заставляеть нѣсколько выпучиваться среднія и въ особенности нижнія части боковыхъ стѣнокъ призмъ. Вертикальное давленіе порождаетъ горизонтальное. Размѣры этого бокового давленія, по изслѣдованіямъ Пуассона [Poisson] и Вертгейма [Guillaume Wertheim], при прочномъ сопротивленіи твердаго вещества равно 1/3-1/2 вертикальнаго давленія; оно возрастаетъ до 2/3 съ увеличеніемъ давленія и, наконецъ, когда подъ высокимъ давленіемъ тѣло пріобрѣтаетъ текучесть, боковое давленіе сравнивается съ вертикальнымъ. Это боковое давленіе играетъ существенную роль въ опредѣленіи величины тренія при вертикальныхъ движеніяхъ предѣльныхъ призмъ.
Итакъ твердая оболочка земли не можетъ держаться напряженіемъ однѣхъ молекулярныхъ силъ: для поддержанія ея въ ея положеніи необходимо гидростатическое давленіе снизу.
Если бы подъ корою была жидкость меньшаго удѣльнаго вѣса, чѣмъ кора, то мы имѣли бы случай неустойчиваго расположенія массъ. Скаловишіеся участки коры стали бы тонуть, а легкая жидкость всплывала бы на поверхность. Не можетъ быть подъ корой жидкость одинаковой плотности съ корой, такъ какъ въ этомъ случаѣ не могли бы существовать обширные выступы (материки, плоскогорья, горные кряжи) въ литосферѣ, ибо эти твердые участки литосферы, не имѣя возможности держаться собственнымъ напряженіемъ молекулярныхъ силъ, должны были бы погружаться въ магму, пока не исчезли бы выступы, подобно тому, какъ не могутъ плавать какіе нибудь твердыя тѣла, выдаваясь надъ жидкостью, у которой плотность таже, что и у плавающихъ тѣлъ. Слѣдовательно, подкоровая магма должна быть тяжелѣе литосферы. Въ этомъ случаѣ твердая кора устойчиво можетъ плавать на магмѣ, подобно тому, какъ ледъ плаваетъ на водѣ. Въ пользу того, что литосфера легче подкоровой магмы, имѣются и другія данныя. Во первыхъ, удѣльный вѣсъ литосферы около 2,65, а средняя плотность земного шара 5,5-5,6. Очевидно, въ глубинѣ земли находятся болѣе тяжелыя вещества, чѣмъ въ наружныхъ частяхъ земли. Съ этимъ вполнѣ гармонируетъ тотъ фактъ, что съ глубиной не убываетъ, а возрастаетъ (до извѣстнаго предѣла) ускореніе силы тяжести. Во вторыхъ, какъ указываютъ Добрэ и Лазо, тяжелыя оливиновыя породы должны играть важную роль въ составѣ глубинныхъ породъ, что доказывается частымъ нахожденіемъ оливина въ метеоритахъ и залеганіемъ оливиновыхъ породъ, которыя подстилаютъ граниты. А такъ какъ эти глубинныя тяжелыя породы произошли отъ застыванія верхнихъ слоевъ магмы, то и подъ ними должна быть основная тяжелая магма. Въ третьихъ, извѣстны огромнѣйшія изліянія основной магмы, какъ въ Деканѣ, занимающія площадь превосходящую Францію и достигающія мощности 1 километра, что говоритъ въ пользу того, что въ глубинѣ земли имѣется богатѣйшій источникъ основной магмы. Въ четвертыхъ, земной магнетизмъ даетъ также опредѣленныя указанія на этотъ счетъ. Если бы земной шаръ состоялъ внутри даже изъ желѣза, то всетаки барисфера была бы неспособна намагничиваться, такъ какъ желѣзо теряетъ свои магнитныя свойства уже при 785°, а магнитный желѣзнякъ при 535°. Поэтому сгущеніе магнитныхь силовыхъ линій должно быть внутри земной коры. Что дѣйствительно имѣютъ связь магнитныя силовыя линіи съ тектоникой земной коры доказывается изогнутіе изогонъ въ Японии во впадинѣ, прорѣзывающей поперегъ островъ Нипонъ, въ Парижскомъ бассейнѣ и др. мѣстахъ. А такъ какъ ни известняки, ни глинистые сланцы, ни мергели, ни кварциты, ни граниты, ни гнейсы неспособны сгущать магнитныя силовыя линіи, то мы должны предположить, что нижніе слои литосферы образовались отъ застывания тяжелой основной магмы, богатой желѣзомъ или базальтовой лавы. (Опыты Меллони показываютъ, что базальты способны намагничиваться). Слѣдовательно, подъ литосферой должна лежать основная тяжелая магма, такъ какъ процессъ затвердѣнія охватилъ уже ея верхніе слои. Можно было бы еще умножить доказательства, но считаемъ это излишнимъ.
Итакъ подкоровая магма плотнѣе земной коры. Это дѣлаетъ возможнымъ плаванье коры на магмѣ. Разъ тѣло плаваетъ, то оно должно подчиняться закону Архимеда: вѣсъ вытѣсненной жидкости долженъ равняться вѣсу плавающаго тѣла. Чѣмъ больше выдается изъ жидкости плавающее тѣло, тѣмъ глубже долженъ быть его фундаментъ, сидящій въ жидкости. Поэтому континенты, полуострова, острова (если они превосходятъ размѣрами 1 кв. кил.) плаваютъ на магмѣ подобно айсбергамъ въ Ледовитомъ океанѣ, будучи погружены своимъ основаніемъ тѣмъ глубже въ магму, чѣмъ выше вздымаются надъ дномъ океана. Отсюда мы проходимъ къ заключеню, что нижняя сторона литосферы имѣетъ неровности: выступамъ на земной поверхности соотвѣтствуютъ выпуклины снизу, впадинамъ сверху - впадины снизу. Слѣдовательно литосфера далеко неодинаковой толщины: максимальной толщины она достигаетъ въ области материковъ и горъ и минимальной подъ океанами и особенно въ глубочайшихъ океаническихъ впадинахъ.
Для простоты разсчетовъ примемъ землю за правильный шаръ. Проведемъ мысленно внутри земли сферическую поверхность, концентрическую земной поверхности и касательную къ самому глубокому подкоровому выступу. Назовемъ ее основной изобарической поверхностью. Она раздѣлитъ земной шаръ на наружный коровый слой, состоящій изъ океанических водъ, литосферы и нѣкотораго количества магмы межъ подкоровыми выступами литосферы, и на огненно жидкое ядро. Жидкая масса этого ядра будетъ въ равновѣсіи, когда давленіе въ изобарической поверхности будетъ = 0; она тоже будетъ въ равновѣсіи, если каждая единица ея поверхности будетъ испытывать одно и то же давленіе. А это будетъ имѣть мѣсто тогда, когда вѣсъ каждаго вертикальнаго столба вещества, имѣющаго въ основаніи 1 кв. кил., или вѣсъ коровой предѣльной призмы будетъ одинъ и тотъ же. Вотъ основное условіе равновѣсія предѣльныхъ призмъ.
Одна предѣльная призма $PQRS$ (рис. 3) будеть стоять только изъ литосферы, другая $KLMN$ - изъ литосферы и магмы, третья $ABCD$ изъ магмы, литосферы и слоя океаническихъ водъ. Несмотря на различіе состава, вѣсъ каждой призмы долженъ быть одинъ и тотъ же. Это даетъ намъ легкій способъ найти зависимость межъ глубиной ($x$) подкороваго фундамента, средней глубиной ($a$) океановъ и высотой ($h$) нагорья надъ уровнемъ моря. Обозначимъ черезъ $d$ плотность литосферы, черезъ $\delta$ - плотность магмы, черезъ $H$ – среднюю толщину океанической литосферы. Тогда должно существовать равенство:
$a \cdot 1 + Hd + x\delta = d (h+a+H+x)$;
откуда
$x = \frac{hd + a(d-1)}{\delta-d}$
Въ этой формулѣ $h$ поддается непосредственному измѣрѣнію; $a = 3,8$ килом. Что же касается $d$ и $\delta$, то эти величины приблизительно намъ извѣстны, и сомнѣнія возможны только въ десятыхъ доляхъ плотности. Такъ среднюю плотность литосферы, мы не можемъ принять меньше 2,5 и больше 2,8. Что касается плотности магмы, то о ней мы можемъ судить по плотности базальтовъ, габбро и оливиновыхъ породъ, и она содержится межъ 3,1 и 3,5.
Минимальныя значенія для $x$ получимъ тогда, когда возьмемъ минимальную плотность для литосферы т. е. 2,5 и максимальную для магмы 3,5. Въ этомъ случаѣ
$x = 2,5h+ 5.7$ килом.
Эта формула даетъ минимальную величину для подкоровыхъ выступовъ.
Если мы примемъ наружную и внутреннюю поверхность литосферы, лежащей подъ океанами, за начало счета для надкоровыхъ и подкоровыхъ выступовъ и впадинъ, то глубочайшей морской впадинѣ въ 5,8 килом (4) будетъ соотвѣтствовать по минимальной оцѣнкѣ ($d = 2,5; \delta = 3,5$) впадина на нижней поверхности литосферы въ 8,7 килом. Среднему подъему материковъ на 4,5 килом. отъ дна океановъ (или 0,7 килом. оть уровня моря) фундаментъ въ 7,4 килом.; плоскогорью въ 6 килом. высоты надъ уровнемъ моря - выпуклина снизу въ 20,7 килом.; высочайшей вершинѣ въ 8,8 килом. — выступъ снизу въ 27,8 килом. Однимъ словомъ рельефъ внутренней поверхности литосферы есть какъ бы зеркальное изображеніе рельефа наружной поверхности, только контуры этого изображенія удлинены въ вертикальномъ направленіи и нѣсколько смягчены, округлены.
Если взять разницу плотностей литосферы и магмы менѣе значительную, то мы будемъ имѣть болѣе вѣроятную величину подкоровыхъ выступовъ. Комбинируя на разные лады плотности литосферы $d$ и магмы $\delta$
| $d$ | $\delta$ |
| 2,8 | 3,5 |
| 2,7 | 3,4 |
| 2,6 | 3,3 |
| 2,5 | 3,2 |
мы найдемъ наиболѣе вѣроятную глубину материковаго фундамента в 11-12 километровъ. Если взять $d = 2,6$ и $\delta = 3,3$, то для глубины подкоровыхъ фундаментовъ будемъ имѣть
$x = 3,71h + 8,69$ килом.,
гдѣ $h$ высота нагорья надъ уровнемъ моря въ килом.
При разсчетѣ наиболѣе вѣроятныхъ величинъ для подкоровыхъ выступовъ мы не беремъ минимальной разницы плотностей, какъ 2,8 и 3,2 или даже 3,1 т. е. въ 0,3-0,4, потому что выступы на земной поверхности обусловлены главнымъ образомъ разностью плотностей межъ верхними и средними слоями литосферы и плотностью тяжелой основной магмы, а эта разница приблизительно равна 0,6-0,7. Хотя нижніе слои литосферы и образовались отъ застыванія верхнихъ слоевъ основной магмы, но они почти не вліяютъ на высоту горъ и подкоровыхъ фундаментовъ, что легко понять изъ слѣдующаго факта. Если къ пробкѣ, плавающей на водѣ, приклеить снизу пластинку изъ какого либо вещества съ удѣльнымъ вѣсомъ = 1, то пробка отъ этого не опустится глубже, чѣмъ сидѣла раньше.
Сдѣлавши разсчеты для наиболѣе вѣроятныхъ подкоровыхъ выступовъ (т. е. полагая $x = 3,71h + 8,69$ килом.), найдемъ.
| Глубина материковаго фундамента | . . = 11.28 килом. |
| Глубина фундамента нагорья въ 5 кил. высоты надъ уровн. моря | . . = 27,24 килом. |
| Глубина фундамента высочайшей горы въ 8,8 килом. | . . = 41,49 килом. |
| Глубочайшая впадина на нижней поверхности литосферы | . . = 13,2 килом. |
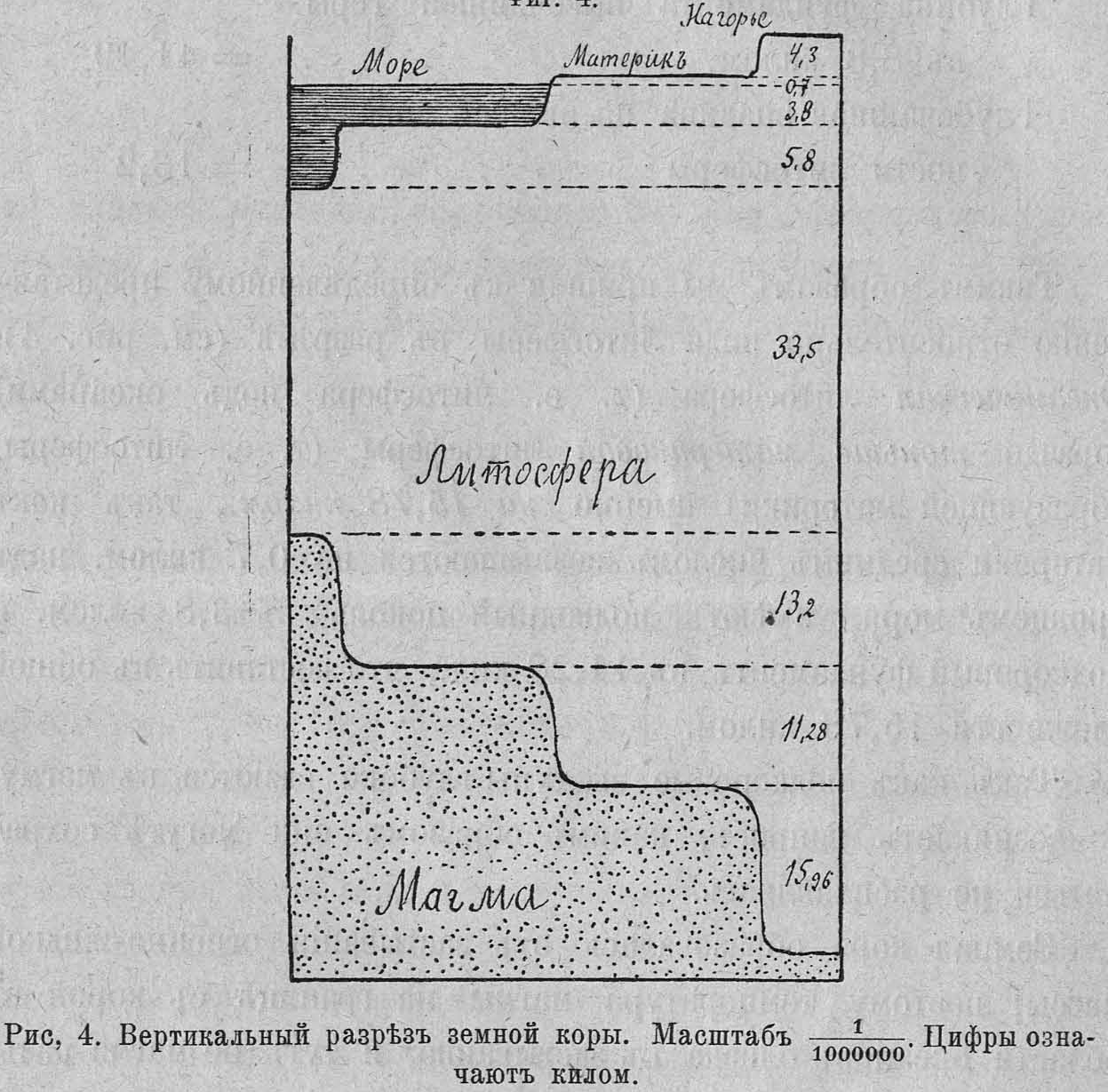
Такимъ образомъ мы пришли къ опредѣленному представленію относительно вида литосферы въ разрѣзѣ (см. рис. 4). Океаническая литосфера (т. е. литосфера подъ океанами) гораздо тоньше материковой литосферы (т. е. литосферы, образующей материки) именно на 15,78 килом., такъ какъ материки среднимъ числомъ возвышаются на 0,7 килом., надъ уровнемъ моря, имѣютъ подводный цоколь въ 3,8 килом., и подкоровый фундаментъ въ 11,28 кил., что составитъ въ общей сложности 15,78 килом.
Такъ какъ подкоровые выступы глубоко вдаются въ магму, то возникаетъ вопросъ, какимъ образомъ они могутъ сохраняться не расплавляясь.
Земная кора образовалась отъ застыванія огненно-жидкой массы; поэтому температура магмы на границѣ съ корой въ области океановъ близка къ застыванію, и тутъ не магма разъѣдаетъ кору, а напротивъ идетъ наростаніе коры на счетъ магмы, такъ что здѣсь о раствореніи не можетъ быть и рѣчи. Съ глубиной температура магмы наростаетъ, но изъ этого еще не следуѣтъ, что невозможно существованіе подкоровыхъ выступовъ. Во первыхъ, известно, что лава можетъ оставаться жидкой при болѣе низкой температурѣ, чѣмъ температура плавленія той же лавы. Такъ опыты съ лавами Везувія и Этны показали, что для расплавленія застывшей лавы ее нужно нагрѣть на 50-100° выше той температуры, при которой она была еще въ жидкомъ состояніи. Во вторыхъ, опыты съ разъѣданіемъ минераловъ лавами показываютъ, что онѣ обнаруживаютъ замѣтное растворяющее дѣйствіе, когда температура лавы превосходитъ на 200° температуру ея плавленія (Doelter. Petrogenesis, стр. 16). Слѣдовательно, возможно существованіе подкоровыхъ выступовъ или фундаментовъ, въ особенности, когда они занимаютъ обширныя площади. Но слишкомъ глубокіе выступы будутъ расплавляться, и тѣмъ самымъ кладется предѣлъ для возможныхъ высотъ горъ. Фундаменты подъ очень высокими горами отчасти растворяются, давая начало кислой и средней магмѣ, питающей вулканы.
Кромѣ доказательствъ, основанныхъ на соотношеніи молярныхъ и молекулярныхъ силъ, относительно неодинаковой толщины литосферы океанической и материковой, имѣется цѣлый рядъ другихъ доказательствъ.
1) Такъ какъ литосфера плаваетъ на магмѣ, то переносъ вещества съ однихъ участковъ на другіе вызываетъ вертикальныя движенія въ литосферѣ. Нагружаемые участки будутъ опускаться, разгружаемые подниматься. Разгрузка и нагрузка предѣльныхъ призмъ въ широкихъ размѣрахъ производится дѣятельностью воды. Подъ тяжестью отлагающихся осадковъ дно морское осѣдаетъ, опускается; наоборотъ, размываемая суша всплываетъ вверхъ, подставляя все новые и новые слои атмосфернымъ вліяніямъ. Какъ опусканіе, такъ и поднятіе ограничено извѣстными предѣлами - глубиною подкоровыхъ фундаментовъ.
Весьма не трудно найти общее выраженіе для возможной толщины ($y$) осадковъ, отлагающихся въ морѣ глубиною въ $\alpha$ килом. Именно
$y = \frac{\alpha(\delta+1)}{\delta-d} = 3,29 \alpha$
Т. е. чтобы выполнить осадками морской бассейнъ при опусканіи морского дна нужна толща осадковъ превосходящая глубину моря въ 3,29 раза. Соотвѣтственно этому получаются слѣдующія возможныя максимальныя толщи осадковъ для различныхъ глубинъ морей:
| Океаническія глубины въ килом. | Максим. толщи осадковъ въ килом. |
| 10 | 32.89 |
| 8 | 26,29 |
| 6 | 19,72 |
| 4 | 13,15 |
| 3,8 | 12,49 |
Этотъ теоретическій выводъ хорошо согласуется съ дѣйствительно ноблюдаемой максимальной толщиной осадковъ отложеній. Такъ общую мощность архейскихъ образованій въ Богеміи и въ Сѣверной Америкѣ оцѣниваютъ приблизительно въ 30 килом. (хотя точное опредѣленіе толщины этихъ образованій представляетъ большія затрудненія). Болѣе точныя данныя имѣются для толщи слоевъ, образующихъ Скалистыя горы, - именно 18 килом. Общая толщина отложеній Донецкаго бассейна 15 килом. Въ Гималаяхъ и Аппалахскихь горахъ мощность пластовъ въ 10-12 килом. Возможность отложенія такихъ большихъ толщь свидѣтельствуетъ объ опусканіи морского дна на 10 килом. и болѣе, а это движеніе съ механической точки зрѣнія допустимо только тогда, когда имѣется разница въ глубинѣ подкоровыхъ фундаментовъ въ 10 и болѣе километровъ.
2) Такъ какъ материковая литосфера на 15,78 килом. толще океанической, то материки отличаются огромною устойчивостью во времени. Недостаточно атмосфернымъ осадкамъ смыть выдающуюся часть суши надъ уровнемъ моря, чтобы она сдѣлалась добычей океана. По мѣрѣ смыванія верхнихъ пластовъ подкоровой фундаментъ всплывая выдвигаетъ болѣе глубокіе слои вверхъ, и этимъ поддерживается существованіе материка. Восходящія движенія коры объясняютъ намъ фактъ залеганія глубинныхь породъ на земной поверхности.
3) Складчатыя горы всегда зарождаются въ области океановъ, а не на континентахъ, что вполнѣ понятно, такъ какъ океаническая литосфера гораздо тоньше материковой и вслѣдствіе этого представляетъ меньше сопротивленія образованію складокъ.
4) Древніе массивы оказываютъ задерживающее вліяніе на развитіе молодыхъ складокъ, которыя либо останавливаются предъ массивомъ, встрѣтившимся на пути, либо огибаютъ его, но не пересѣкаютъ. Это вліяніе древнихъ массивовъ, какъ Севенское плато, Чешскій массивъ, Шварцвальдъ, Вогезы, Мезета, Родопъ и т. д. можно отлично видѣть на ходѣ различныхъ новѣйшихъ горныхъ системъ: Юры, Альпъ, Карпатовъ, Балкановъ, Тянь-Шаня и др. Такъ какъ литосфера въ области горъ достигаетъ огромной толщины, превосходя океаническую литосферу на 18-20 килом. и болѣе, то неудивительно, что молодыя складки останавливаются предъ существующими горами, какъ передъ стѣной.
5) Въ области океановъ тяжелая магма лежитъ гораздо ближе къ земной поверхности, чѣмъ подъ материками. Поэтому мы можемъ разсчитывать найти на океаническихъ островахъ большее ускореніе тяжести, чѣмъ теоретически расчитанное для даннаго мѣста. Дѣйствительно, Defforges находитъ, что на островахъ ускореніе тяжести вообще превосходитъ среднее значеніе, соотвѣтствующее данной широтѣ. На уединенныхь островахъ маятникъ, которымъ пользуются для измѣренія земныхъ ускореній, качается быстрѣе. На Бонинскихъ островахъ секундный маятникъ дѣлаетъ въ сутки 11,8 ударами больше, чѣмъ надо было бы ожидать, судя по георафическому положенію мѣста. На о. Уаланъ число лишнихъ ударовъ 8,7, на о. Св. Елены - 6,6, Ильдефрансѣ - 9,9, на Фернандо-Норонья - 9,4; на Шпицбергенѣ - 4,3. Наоборотъ, нигдѣ такого ускореннаго качанія маятника на берегахъ материковъ не замѣчается.
6) Наблюденія Штернека, произведенныя при помощи усовершенствованнаго маятника въ Тиролѣ, Чехіи, Карпатахъ надъ ускореніемъ тяжести, и вычисленія Гельмерта показали, что дѣйствіе твердыхъ массъ земли въ большей или меньшей степени уничтожается вслѣдствіе меньшей плотности земной коры подъ материками. Большимъ скопленіемъ массъ на поверхности, образующимъ горы и материки, соотвѣтствуютъ внутри земли извѣстные недочеты массъ. Гельмертъ говоритъ, что существуетъ какая то постоянная причина, благодаря которой подъ материками и горами повсюду наблюдаются недочеты массъ или залеганіе болѣе легкихъ пластовъ. Если сдѣлать поперечный вертикальный разрѣзъ черезъ Апеннинскій полуостровъ на уровнѣ о. Капри и начертить кривую тяготѣнія, то окажется, что на Капри и Адріатическомъ морѣ кривая приподнята, а въ области Апеннинъ понижена. Эти факты краснорѣчиво свидѣтельствуютъ, что подъ материками и горами имѣются фундаменты изъ болѣе легкаго вещества, чѣмъ магма, и что само существованіе материковъ связано съ наличностью подкоровыхъ фундаментовъ.
Есть и другія доказательства въ пользу большей толщины материковой литосферы, но и приведенныхъ фактовъ, мнѣ кажется, достаточно для того, чтобы окончательно признать неодинаковую толщину океанической и материковой литосферы.
До сихъ поръ мы старались выяснить только относительную разницу въ толщинѣ океанической и материковой литосферы. Теперь же попытаемся опредѣлить абсолютную толщину той и другой. Укажемъ три различныхъ способа этого опредѣленія, исходя 1) изъ аномалій силы тяжести на земной поверхности и максимальной толщи осадковъ, 2) изъ геотермическаго градіента и растворяющихъ свойствъ магмы; 3) изъ сокращенія земной поверхности при горообразованіи.
1) Аномаліи тяжести охватывають только поверхностный слой земли: литосферу и ту пограничную область, гдѣ подкоровые выступы внѣдряются въ магму, т. е. коровый слой до основной изобарической поверхности. Мы не можемъ ожидать встрѣтить крупныя включенія (будь то жидкіе или твердые), рѣзко отличающіяся по плотности отъ магмы въ жидкой магмѣ, такъ какъ легкія вещества всплыли бы подъ кору, болѣе тяжелыя - опустились бы внизъ - вглубь. Ясно, что чѣмъ глубже лежитъ возмущающая причина, тѣмъ на болѣе далекое разстояніе отъ эпицентра возмущенія будутъ замѣчаться аномаліи на земной поверхности, и тѣмъ постепеннѣе будетъ ея затуханіе. По изслѣдованіямъ Мессершмитта причины, производящая аномаліи тяжести на земной поверхности лежатъ никакъ не глубже 200 килом. Поэтому мы не можемъ принять материковую литосферу слишкомъ толстой, напр., въ 180 кил., такъ какъ въ этомъ случаѣ подкоровые выступы горъ и нагорій вдавались бы въ магму больше, чемъ на 200 килом. (отъ земной поверхности), и следовательно аномаліи тяжести простирались бы более, чѣмъ на 200 килом., что не оправдывается наблюденіями. Поэтому, если мы примемъ толщину материковой литосферы въ 110-120 килом., то мы приблизимся къ предѣлу, указанному Мессершмиттомъ, такъ какъ къ этой величинѣ мы должны еще прибавить подкоровые фундаменты горъ и нагорій. 110-120 килом. будетъ высшій предѣлъ для толщины материковой литосферы. Низшій предѣлъ намѣчается максимальной толщей осадковъ. Намъ известны толщи осадковъ въ 30 килом. Если подобныя толщи могли собраться въ складки, то мы можемъ заключить, что и другія части океанической литосферы имѣютъ приблизительно такую же толщину, ибо складки образуются въ мѣстахъ наименьшаго сопротивленія. А такъ какъ материковые литосферы по крайней мѣрѣ на 12 килом. толще океанической, т. е. минимумъ равна 42 килом., то отсюда мы имѣемъ предѣлы, межъ которыми содержится толщина материковой литосферы: Минимумъ 42 килом. - максимумъ 110 - 120 килом.
2) Другой способъ опредѣленія толщины земной коры основанъ на геотермическомъ градіентѣ, который среднимъ числомъ = 38 метрамъ. Если бы съ глубиной величина геотермическаго градіента оставалась неизмѣнной, то подъ материками толщина литосферы была бы не болѣе 33·1500 = 49500 метр. = 49,5 килом., такъ какъ при температурѣ въ 1500° горныя породы, несмотря на давленіе въ 13000 атмосферъ, которое повысило бы температуру плавленія на 117°-390°, всетаки находились бы въ жидкомъ состоянии. Въ дѣйствительности геотермическій градіентъ возрастаетъ съ глубиною. Въ пользу этого говорятъ не только теоретическія соображенія, но и опыты Бишофа въ Боннѣ съ остываніемъ раскаленнаго базальтоваго шара, и наблюденія надъ наростанемъ температуры въ буровыхъ скважинахъ съ глубиной. Это удлиненіе геотермическаго градіента съ глубиной подмѣтилъ еще Араго, а позднѣе оно было неоднократно констатировано.
Поэтому цыфра 49,5 килом. представляетъ минимумъ для толщины материковой литосферы; въ дѣйствительности эта толщина значительнѣе, благодаря приросту геотермическаго градіента съ глубиной. Прежде всего замѣтимъ, что врядъ ли онъ возрастаетъ въ земной корѣ до 100 метровъ. Дѣло въ томъ, что если-бы мы могли имѣть буровую скважину сквозь всю толщу земной коры, то возрастаніе температуры отъ одного динамическаго нагрѣванія воздуха вслѣдствіе его сжатія дало бы повышеніе температуры въ 1° на 100 метр. А въ земной корѣ имѣются трещины, по которымъ газы могутъ проникать вглубь. Сверхъ того, опусканіе вглубь какого либо пласта должно вызвать нагрѣваніе его приблизительно на 1° на 90-100 метр.
Поэтому у насъ есть основаніе ожидать, что геотермическій градіентъ въ подкоровыхъ фундаментахъ будетъ менѣе 100 метр. Чтобы найти числовую величину прироста геотермическаго градіента, я воспользовался слѣдующими соображеніями. Такъ какъ материки отличаются огромною устойчивостью во времени, то, очевидно, ихъ подкоровые фундаменты прочно сопротивляются растворяющему дѣйствію магмы. Средняя глубина этихъ фундаментовъ 11—12 кил. Если магма обнаруживаетъ замѣтное растворяющее дѣйствіе, когда она нагрѣта на 200° выше температуры ея плавленія, то слѣдуетъ положить, что материковые фундаменты погружены въ магму нагрѣтую менѣе 200° (5) противъ температуры верхняго слоя магмы подъ океанической литосферой. Отсюда мы заключаемъ, что геотермическій градусъ въ материковыхъ фундаментахъ не долженъ превышать 12000/500 = 60 метров. Такъ какъ вблизи земной поверхности онъ = 33 метр., то слѣдовательно онъ возросъ на 27 метровъ, а прирость на 1° среднимъ числомъ будетъ 27/1500 метр. Допуская, что наростаніе геотермическаго градуса съ глубиною идетъ равномѣрно, мы находимъ такую величину для толщины ($H_1$) материковой литосферы:
$H_1 = 33 \cdot 1500 + \frac{24}{1500} \cdot \frac{1500^2}{2} = 49500 + 20250 = 69750$ метр. $= 69,75$ килом.
Это число лежитъ какъ разъ межъ предѣлами: 42 миним., и 110-120 кил. макс., которые мы нашли раньше.
3) Наиболѣе точные результаты относительно толщины литосферы мы можемъ получить, исходя изъ цыфры сокращенія земной поверхности при горообразованіи. Если разломить пластинку изъ воска, слегка нагрѣтъ плоскости разлома, снова сложить оба куска нагрѣтыми частями и слегка ихъ сдавить, чтобы склеить пластинку, то мы замѣтимъ, что по линіи разлома сверху и снизу пластинки образовался валикъ изъ воска, а поверхность пластинки нѣсколько уменьшилась. Нѣчто подобное происходитъ и при образованіи горъ. Когда ядро земли сжимается, литосфера становится черезчуръ просторной и, приближаясь къ центру земли въ слѣдь за сократившимся ядромъ, развиваетъ сильное боковое давленіе. Въ мѣстахъ наименьшаго сопротивленія одна часть литосферы наѣзжаетъ, надвигается на другую, вслѣдствіе чего въ океанической литосферѣ возникаетъ на большемъ или меньшемъ протяженіи утолщеніе, которое въ поперечномъ разрѣзѣ имѣетъ видъ, изображенный на рис. 5. Если убыль океанической литосферы равна $n$ кв. кил., то возникаетъ избытокъ объема $nH$, гдѣ $H$ есть толщина океанической литосферы. Этотъ избытокъ и идетъ на образованіе надкорового вздутія (горной системы) и подкороваго фундамента. Легко видѣть, что этотъ избыточный объемъ
$nH = s(a+h)+x\cdot s = s(a+h+x)$,
гдѣ $h$ - средняя высота нагорья надъ уровнемъ моря, $a$ - глубина океана, $x$ — глубина фундамента, $s$ - площадь, занятая горной системой. Зависимость фундамента ($x$) отъ высоты нагорья ($h$) опредѣляется, какъ мы уже знаемъ, такой формулой $x = \frac{s}{n}\frac{hd + a(d-1)}{\delta-d}$, гдѣ $d$ - средн. плотность литосферы, $\delta$ - плотность магмы.
Подставляя $x$ въ предыдущую формулу, мы будемъ имѣть:
$H = \frac{s}{n}\frac{h\delta + a(\delta-1)}{\delta-d}$
Таковъ законъ, связующій толщину океанической литосферы ($H$) со степенью сокращенія земной поверхности при горообразованіи, высотою горъ, плотностями литосферы ($d$) и магмы ($\delta$) и глубиной ($a$) океана.
Высота горъ ($h$) и глубина ($a$) океановъ опредѣляются непосредственнымъ измѣреніемъ съ достаточной точностью. Средняя плотность литосферы и магмы, какъ мы говорили, колеблется въ узкихъ предѣлахъ, и мы приняли какъ наиболѣе вѣроятныя величины для плотн. литосф. $d = 2,6$ и магмы $\delta =3,3$; $n+s$ представляютъ собою поверхность, если расправить всѣ складки въ горной системѣ, $s$ - площадь, занятая горной системой, $n$ - убыль первоначальной площади. Подставляя численныя значенія въ законъ горообразованія, найдемъ
$H = \frac{s}{n} (h + 3,8 + 3,71h + 8,69) = \frac{s}{n}(4,71h + 12,49)$
Геймъ опредѣлилъ довольно точно степень сокращенія земной поверхности при образованіи Юрской системы и менѣе точно при возникновеніи Альпійской системы.
Разстояніе межъ Женевскимъ озеромъ, лежащимъ на южной окраинѣ, и мѣстечкомъ С. Клодъ, лежащимъ на сѣверной окраинѣ системы юрскихъ складокъ, равно 16800 метровъ. По распрямленіи, выглаживаніи складокъ это разстояніе увеличилось бы на 5200 метр., т. е. до сокращенія первоначальное разстояніе было равно 22000 метр. Слѣдовательно $\frac{s}{n} = \frac{16800 \cdot L}{5200 \cdot L} = \frac{42}{13}$, гдѣ $L$ – длина цѣпи. Средняя высота Юрской системы, судя по гипсометрическимъ картамъ, высотѣ положенія долинъ и высотѣ горъ, не менѣе 0,8 километр. Подъ средней высотой слѣдуетъ разумѣть общій подъемъ суши подъ Юрской системой, если все вещество горъ разложить ровнымъ слоемъ на площади, занятой Юрской системой.
Подставляя численныя значенія, мы найдемъ толщину океанической литосферы, давшей начало Юрской системѣ:
$H = \frac{42}{13} (4,71 \cdot 0,8 + 12,49) = 52,53$ килом.
А такъ какъ материковая литосфера, какъ мы нашли раньше, на 15,78 кил. толще океанической, то слѣд. толщина материковой литосферы = 52,53 + 15,78 = 68,31 килом.
Эта цифра почти тождественна съ той, которую мы нашли, когда исходили изъ геотермическаго градіента и растворяющихъ свойствъ магмы. Хорошее согласіе цыфръ позволяеть намъ относиться съ довѣріемъ къ полученнымъ результатамъ.
Разъ мы опредѣлили толщину литосферы ($H$), то мы можемъ воспользоваться закономъ горообразованія $H = \frac{s}{n}(4,71h + 12,49)$ для опредѣленія степени сокращенія земной поверхности при возникновеніи той или другой системы. Такъ какъ въ приведенной формулѣ $h$ и $s$ легко поддаются непосредственному измѣренію, то при извѣстномъ $H$ можно вычислить $n$ и обратно. Такимъ образомъ открывается возможность не только провѣрить самую формулу, но и установить болѣе точно ея численные коэффиціенты. Провѣримъ этотъ законъ на Альпійской системѣ, т. е. найдемъ теоретически, насколько километровъ сузилась полоса земной поверхности при образованіи Альпъ. Для этого намъ нужно знать ширину Альпійской системы (ширина среднихъ и восточныхъ Альпъ = ок. 300 килом.) и среднюю высоту Альпійской системы. По Лейпольдту она = 1,2 килом. Т. е. если все вещество Альпъ разложить ровнымъ слоемъ на площади, занятой Альпійской системой, (на 300.000 кв. кил.), то высота этого слоя будетъ 1,2 кил. Обозначимъ черезъ $x$ число килом., на которое сузилась полоса земной поверхности при образованіи Альпъ.
$\frac{s}{n} = \frac{300 \cdot L}{x\cdot L} = \frac{300}{x}$, гдѣ $L$ длина цѣпи
Отсюда имѣемъ:
$52,5 = \frac{300}{x} (4,71 \cdot 1,2+12,49)$; откуда $x$=104 килом.
Полученная нами цыфра должна быть нѣсколько ниже дѣйствительной, такъ какъ Альпы уже подверглись размыванію (по Дюттону Финстерааргорнъ понизился на 1 килом.), вслѣдствіе чего ихъ теперешняя средняя высота нѣсколько ниже первоначальной, такъ что сокращеніе на нѣсколько километровъ будеть больше найденной цыфры – приблизительно 109-110 килом.
Геймъ непосредственно измѣрилъ, насколько сузилась полоса земной поверхности при образованіи Альпійской системы и нашелъ эту убыль ширины равной 120 килом. Такимъ образомъ, теоретически найденная мною величина сжатія 109-110 кил. удовлетворительно согласуется съ числомъ 120 найденнымъ непосредственнымъ измѣреніемъ (6).
Весьма желательно было бы провѣрить законъ горообразованія и на другихъ горныхъ цѣпяхъ, конечно, молодыхъ, не успѣвшихъ еще подвергнуться сильному размыванію. При этомъ не слѣдуетъ думать, что въ каждомъ случаѣ мы должны получить въ точности цыфру океанической литосферы = 52,5 кил. Эта цыфра есть средняя толщина океанич. литосферы, которая въ дѣйствительности бываетъ то тоньше, то толще. Толщина же литосферы, собирающейся въ складки, вѣроятно, окажется нѣсколько ниже средней, такъ какъ складки возникаютъ въ мѣстахъ наименьшаго сопротивленія, т. е. тамъ, гдѣ кора потоньше.
На основаніи всѣхъ выше приведенныхъ разсчетовъ размѣры земной коры представляются въ слѣдующемъ видѣ:
| Гидросфера | Литосфера | |
| Средняя толщина при равномѣрномъ распредѣл. по земн. поверхн., килом. | 2,7 | 56,72 |
| Объемъ, милліоны куб. килом. | 1417,4 | 28600,6 |
| Объемъ земного шара = 1, доля объема | 1/764 | 1/37,9 |
| Средняя глубина океановъ, килом. | 3,8 | - |
| Наибольшая глубина в океанѣ, килом. | 9,6 | - |
| Средняя толщина океанической литосферы, килом. | - | 52,5 |
| Средняя толщина материковой литосферы, килом. | - | 68,28 |
| Наибольшая толщина литосферы, килом. | - | 106,6 |
| Наименьшая толщина литосферы, килом. | - | 33,5 |
| Общая толщина земной коры, килом. | 59,42 | |
Нарушеніе равновѣсія въ земной корѣ вызывается разгрузкой и нагрузкой предѣльныхъ призмъ (переносомъ вещества съ однихъ участковъ коры на другіе), передвиженіями и колебаніями магмы, вызываемыми движеніями коры, отчасти и другими причинами, сокращеніемъ ядра земли отъ охлажденія. Это ведетъ къ вертикальнымъ движеніямъ (образованію грабеновъ, или сбросовыхъ впадинъ, и горстовъ) и горизонтальнымъ движеніямъ, благодаря которымъ возникаютъ утолщенія въ литосферѣ, покрытыя снаружи складчатами горными цѣпями.
Такъ какъ материки представляють собою утолщенную литосферу, а утолщенія въ ней возникаютъ какъ результатъ сокращенія ядра земли, при чемъ наружные слои собираются въ складки, то материки слѣдуетъ разсматривать, какъ образованія производныя отъ горныхъ системъ. Дѣйствительно, ближайшее разсмотрѣніе этого вопроса показываетъ, что материки состоятъ изъ молодыхъ горныхъ системъ, изъ старыхъ, размытыхъ въ различной степени и, наконецъ, изъ горизонтально напластованныхъ осадочныхъ породъ, которыя выполнили тѣ или другіе водные бассейны. Поэтому развитіе материковъ, вѣроятно, происходило такимъ образомъ. Вслѣдствіе сокращенія ядра оть охлажденія сжималась кора, однѣ части ея наѣзжали, надвигались на другія и давали полосы утолщеній: a) надкоровые выступы или параллельныя цѣпи складчатыхъ горъ, и b) подкоровыя выпуклины - фундаменты подъ горными цѣпями. Такимъ образомъ изъ-подъ океаническихъ водъ выдвигались болѣе или менѣе вытянутые гористые острова: къ нимъ примыкали другіе - позднѣйшіе. Бассейны межъ ними выполнялись осадками отъ размыванія прилегающихъ гористыхъ острововъ, и суша наростала. Какую существенную роль играютъ складчатыя горныя системы въ развития материковъ, можно видѣть изъ того, что горы третичнаго возраста дали приращеніе суши по пространству равное цѣлому континенту. Одни Анды Южной Америки вмѣстѣ съ Альпами занимаютъ площадь въ 8,3 милліона кв. кил. т. е. почти 1/2 Новой Голландіи и далеко превосходятъ ее по высотѣ подъема надъ уровнемъ моря. Зная, какую узловатость въ литосферѣ развиваетъ данная убыль земной поверхности, мы можемъ легко сосчитать, какъ будетъ наростать суша при постепенномъ сокращеніи земного радіуса на 1 метр., 5, 100, 1 килом. и т. д.
Для развитія всѣхъ современныхъ континентовъ съ ихъ плоскогорьями, горами, полуостровами и островами достаточно было сокращенія земного радіуса на 261 килом. Такъ какъ въ прежніе геологическіе періоды существовали иные материки, то за историческій періодъ своего существованія земной шаръ сильно уменьшился въ объемѣ: его радіусъ сократился гораздо болѣе, чѣмъ на 261 кил. Вмѣстѣ съ тѣмъ слѣдуетъ, что развитіе суши ведеть къ поднятію уровней морей. Такъ какъ узловалость (утолщения) въ литосферѣ развиваются насчетъ уменьшенія поверхности океанической литосферы, то площадь подъ океанами уменьшается; то же количество воды должно умѣститься на меньшемъ пространствѣ, вслѣдствіе чего толщина воднаго слоя возрастаетъ. Это возрастаніе еще больше увеличивается оттого, что возникшая узловатость вытѣсняетъ океаническія воды съ того мѣста, на которомъ она возникла, такъ что площадь океаническихъ водъ убываетъ. Все это ведетъ къ поднятію уровня морскихъ водъ, которое вызываетъ трансгрессіи моря: воды затопляютъ низменныя мѣста суши. Нижеприведенная таблица даетъ наглядное представленіе о развитіи суши (съ подъемомъ въ 0,7 килом. надъ уровнемъ моря) и трансгрессіяхъ моря.
| Уменьшеніе земнаго радіуса | 1 метръ | 5 | 100 | 1 кил. | 5 | 10 | 50 | 100 | 200 | 261.1 |
| Уменьшеніе земной поверхности, кв. килом. | 160 | 800,5 | 16010 | 160087 | 800186 | 1599743 | 7973584 | 15884336 | 31457000 | 41056000 |
| Уменьшеніе объема земного шара, милліоны куб. килом. | 0,51 | 2,55 | 51,0 | 509,98 | 2548,25 | 5092,5 | 25302,0 | 50208 | 96328 | 127828 |
| Увеличеніе материковой литосферы на счетъ океанической, кв. килом. | 532,3 | 2661,5 | 53230 | 532300 | 2661500 | 5323000 | 26524409 | 52836744 | 104863100 | 136500000 |
| Повышеніе уровня океаническихъ водъ (трансгрессіи моря), метры. | 0,007 | 0,035 | 0,704 | 7,044 | 35,549 | 71,745 | 386,6 | 856,8 | 2185,6 | 3443,5 |
Наконець, слѣдуетъ еще сказать нѣсколько словъ объ аномаліяхъ высотъ. Хотя вѣсъ участковъ коры съ поперечникомъ въ 50, 100 или 500 килом. во много разъ превосходитъ силы сцѣпленія, дѣйствующія въ боковыхъ стѣнкахъ этихъ участковъ, тѣмъ не менѣе эти силы не нуль. Если онѣ въ состояніи преодолѣть весь вѣсъ этихъ участковъ, то онѣ могутъ нѣкоторую долю его поддержать въ положеніи, несоотвѣтственномъ законамъ гидростатики. Напр., если въ какомъ нибудь участкѣ коры, толщиною въ 68 килом., молекулярныя силы могутъ преодолѣть только 1% вѣса этого участка, то возможны уклоненія вверхъ и внизъ отъ положенія, опредѣляемаго гидростатикой на 1/100, т.е. 68000/100 = 680 метровъ. Вслѣдствіе бокового давленія, оттока или притока магмы этотъ участокъ можетъ опуститься или подняться вверхъ на 680 метр. безъ всякаго измѣненія глубины фундамента. Это уклоненіе, вызываемое молекулярными силами, можно назвать аномаліей высотъ. Чѣмъ больше участокъ, тѣмъ слабѣе роль молекулярныхъ силъ, тѣмъ незначительнѣе аномалія. Вотъ размѣры аномалій для участковъ материковой литосферы различныхь діаметровъ:
| Для пл. кругов діам. до, килом. | метр.* |
| 10 | 6800 |
| 50 | 1360 |
| 100 | 680 |
| 1000 | 68 |
| 50000 | 13.6 |
Благодаря этимъ аномаліямъ возможны нѣкоторыя колебанія суши безъ измѣненія глубины ея фундамента: низменность, опускаясь, можетъ превратиться въ неглубокое море и обратно, неглубокое море можеть дать начало сушѣ. Анализъ осадковъ въ петрографическомъ отношеніи, слагающихъ горизонтальныя напластованія равнинъ, показываетъ, что это осадки прибрежные, мелководные или въ крайнемъ случаѣ умѣренныхъ глубинъ. Напротивъ, среди осадковъ, образующихъ складчатыя горы, могутъ встрѣчаться и самыя глубоводныя отложенія. Таковы, напримѣръ, роговики Альпъ, которые состоять изъ панцырей радіолярій и иглъ кремнистыхъ губокъ. Этоть типъ осадка свойственъ очень глубокимъ мѣстамъ современныхъ океановъ.
Не входя въ разсмотрѣніе различныхъ гипотезъ относительно происхожденія континентовъ, считаю нужнымъ сказать нѣсколько словъ о гипотезѣ Дуттона, который полагаетъ, что подъ материками литосфера тоньше, чѣмъ подъ океанами, т. е. высказываетъ взгляды какъ разъ обратные развиваемымъ мною. Онъ полагаетъ, что болѣе тонкіе и болѣе легкіе участки земной коры будутъ легче поддаваться центробѣжной силѣ вращающагося земного шара, чѣмъ участки болѣе тяжелые и болѣе толстые; первые будутъ стремиться вверхъ - удалиться отъ оси вращенія, вторые будутъ оставаться на относительно болѣе близкомъ разстояніи отъ оси вращения, а вмѣстѣ съ тѣмъ и отъ центра земли. Приподнятые участки дали начало континентамъ, впадины - океанамъ. Это разсужденіе ошибочно вслѣдствіе переоцѣнки молекулярныхъ силъ и центробѣжной силы. Согласно Дуттону, жидкое ядро земного шара имѣетъ стремленіе сжаться гораздо больше, чѣмъ оно сжато въ настоящее время. Препятствіемъ для дальнѣйшаго сжатія служитъ твердая кора. Тамъ гдѣ она тоньше и слабѣе, напр., подъ плоскогорьями въ 5 километръ высоты магма удаляется оть центра земли слишкомъ на 10 килом. больше противъ ея теперешняго средняго уровня. Другими словами, небудь земной коры, жидкое ядро сжалось бы еще у полюсовъ на 10 килом. и болѣе, и потому сжатіе жидкаго сфероида земли было бы 1/200 или даже 1/150. А это совершенно ошибочно. При данномъ напряженіи тяжести на поверхности жидкаго сфероида и данной скорости вращенія степень сжатія есть совершенно опредѣленная величина, именно, извѣстная теорема Клеро связываетъ ускореніе тяжести на полюсѣ ($g_b$) и экватор ($g_a$), ускореніе ($F$) центробѣжной силы на экваторѣ и степень сжатія ($\mu$) сфероида (7).
$\mu + \frac{g_b-g_a}{g_a} = \frac{5}{2} \frac{F}{g_a}$
Если мы вставимъ численныя значенія, относящіяся къ земному шару въ формулу Клеро, то взявши разность ускореній на полюсѣ и экваторѣ, согласно Гельмерту, 5,3 сант. въ сек., найдемъ степень сжатія 1/300. Т. е. если бы земля состояла изъ жидкости, она не имѣла бы тенденціи сжаться болѣе, чѣмъ сжата теперь. Если же разность ускореній по другимъ даннымъ взять = 5,01 сантим., то въ этомъ случаѣ сжатіе было бы 1/282, и поверхностные слои на экваторѣ стремились бы удалиться на 1 килом. отъ оси вращенія, а не на 10-15 кил., какъ принимаетъ Дуттонъ. Но и въ этомъ случаѣ, благопріятномъ для гипотезы Дуттона, жидкое ядро земли не имѣло бы тенденціи сжаться, такъ какъ съ глубиной убываетъ центробѣжная сила и возрастаетъ напряженіе силы тяжести, т.е. оба фактора измѣняются такъ, что величина сжатія падаетъ. Отсюда видно, что жидкое ядро земли не имѣетъ тенденціи отталкивать литосферу и сжаться больше, чѣмъ оно сжато теперь; и какъ неудовлетворительна гипотеза Дуттона съ механической точки зрѣнія, такъ и неудовлетворительна въ другихъ отношеніяхъ, напр., какимъ образомъ складчатыя горы зарождаются въ океанахъ, гдѣ литосфера толще и крѣпче и слѣдоват. представляетъ большее сопротивленіе, чѣмъ тонкая материковая литосфера и т. д. (8)
Вмѣстѣ съ тѣмъ будеть не лишнимъ сдѣлать слѣдующую оговорку относительно предѣльныхъ призмъ. Въ своихъ разсчетахъ ради простоты мы приняли землю за правильный шаръ, и соотвѣтственно этому основная изобарическая поверхность была шаровая, и всѣ предѣльныя призмы, если онѣ состояли изъ вещества одинаковой плотности, имѣли одну и ту же высоту. Въ дѣйствительности основная изобарическая поверхность есть элипсоидъ вращенія, опредѣляемый закономъ Клеро. Сжатіе этого элипсоида нѣсколько меньше сжатія земного сфероида. Коровой же слой, т, е. слой, лежащій межъ изобарической поверхностью и наружной поверхностью земли, имѣетъ не одинаковую толщину: на полюсѣ онъ тоньше, на экваторѣ толще. Соотвѣтственно этому высоты предѣльныхъ призмъ больше на экваторѣ, чѣмъ на полюсѣ вслѣдствіе того, что напряженіе тяжести убываетъ по направлению отъ полюса къ экватору, и потому нужно изъ одного и того же вещества, болѣе высокій столбъ (приблизительно на 1/2 километра) на экваторѣ, чѣмъ на полюсѣ для того, чтобы давленіе всякой предѣльной призмы на изобарическую поверхность имѣло одну и ту же величину.
Подведемъ итоги нашему изслѣдованію.
- Земля состоитъ изъ газоваго ядра (сильно сгущенныхъ паровъ), толстаго слоя огненножидкой массы и тонкой (менѣе 1/100 радіуса) твердой оболочки, или литосферы.
Общая форма нашей планеты опредѣляется молярными силами и центробѣжной силой, а молекулярныя силы играютъ третьестепенную роль.
Молекулярныя силы, дѣйствующія въ литосферѣ, не въ состояніи поддерживать крупные участки коры, вслѣдствіе чего нужно признать, что кора плаваетъ на магмѣ, подчиняясь законамъ гидростатики.
Земная кора неодинаковой толщины: подъ дномъ океановъ она тоньше на 15 килом., чѣмъ въ области материковъ.
Внутренній рельефъ литосферы есть зеркальное изображеніе наружнаго рельефа, при чемъ контуры подкорового изображенія нѣсколько вытянуты въ вертикальномъ направленіи, округленны, смягчены.
Участки земной коры размѣрами въ 1 кв. кил. представляютъ собою предѣльныя призмы, т. е. такіе столбики коры, вѣсъ которыхъ какъ разъ равенъ молекулярнымъ силамъ, дѣйствующимъ въ стѣнкахъ столбика и противящихся скалыванію или срѣзыванію по плоскости этихъ стѣнокъ.
Нагрузка предѣльныхъ призмъ ведетъ къ ихъ опусканію, разгрузка - къ поднятію. Эта нагрузка и разгрузка производится главнымъ образомъ дѣятельностью воды, которая смываетъ слои съ однихъ участковъ и отлагаетъ ихъ на другіе.
Опусканіе призмъ можетъ идти только до опредѣленной глубины. Если море $\alpha$ килом. глубиной, то максимальное опусканіе дна будетъ на $2,3\alpha$ кил. или максимальная толща осадковъ для моря глубиною $\alpha$ килом. будетъ $3,3\alpha$ кил.
Сокращеніе барисферы отъ охлажденія вызываетъ образованіе складокъ (утолщеній въ литосферѣ), согласно закону горообразованія.
изъ аномалій тяжести и максимальныхъ толщъ осадковъ: Минимумъ 42 кил. . . . Максимумъ 110-120 кил.
изъ геотермическаго градіента и растворяющихъ свойствъ магмы: 69
изъ сокращенія поверхности при горообразованіи: 68
Толщина океанической литосферы = 52,5 килом.
Материки представляютъ собою обширныя скопленія узловатостей литосферы, происшедшихъ частью вслѣдствіе горообразующихъ процессовъ, частью вслѣдствіе выполненія осадками морскихь и прѣсноводныхъ бассейновъ. Слѣд. материки являются производными образованіями отъ горныхъ системъ.
Колебанія суши и моря вызываются:
a) вертикальнымъ движеніемъ предѣльныхъ призмъ вслѣдствіе нагрузки и разгрузки;
b) образованіемъ складчатыхъ горъ, что съ одной стороны даетъ начало новой сушѣ, а съ другой вызываетъ трансгрессіи моря;
c) вліяніемъ молекулярныхъ силъ, которыми обусловливаются аномаліи высотъ; эти уклоненія тѣмъ меньше, чѣмъ значительнѣе площади, въ которыхъ возникаютъ аномаліи, и чѣмъ тоньше литосфера.
Примѣчания
- Молярныя силы зависятъ оть взаимнаго тяготѣнія матеріальныхъ частичекъ согласно закону Ньютона. Идти назадъ.
При сокращеніи земного радіуса на 1 сантиметръ выдѣлившаяся энергія $W$ будетъ $W = \frac{3}{5} \frac{M^2K}{R(6371\cdot 10^5-1)} = \frac{2244\cdot 10^{36} }{ 6371\cdot 10^5-1} = 35\cdot 10^{29}$ эрговъ = 84·1021 малыхъ калорій. Идти назадъ.
Слѣдуетъ указать, что Геймъ впалъ въ крупную ошибку, заключивъ, что если подъ Альпами полоса земной поверхности съузилась на 120 килом., то и окружность земного шара съузилась на 120 кил. Альпы занимаютъ только 1/36 часть длины большого круга, и если на этой части произошло съуженіе, то отсюда не слѣдуетъ, что это съуженіе распространилось еще на 17/36 дуги большого круга. Идти назадъ.
Абсолютная глубина этой впадины отъ поверхности океана 9,6 килом., средняя глубина океановъ = 3,8 килом. и съ этой глубины ведется счетъ для надкоровыхъ деформацій литосферы. Идти назадъ.
Точнѣе менѣе 240°, если принять во вниманіе повышеніе точки плавленія отъ давления. Идти назадъ.
Новѣйшія работы французскихъ геологовъ даютъ иную схему складокъ въ Альпійской цѣпи – глубоко отличную отъ той, которая построена Геймомъ, и потому нельзя быть увѣреннымъ въ томъ, насколько въ дѣйствительности произошло суженіе полосы литосферы при возникновеніи Альпійской системы. Идти назадъ.
Сжатіе есть отношеніе разности межъ экваторіальнымъ радіусомъ ($a$) и полярнымъ ($b$) къ экваторіальному, т. е. $\mu = \frac{a-b}{a}$; для земли $\mu$ = около 55. Идти назадъ.
Лицъ, интересующихся вопросами механики земли и геофизики, отсылаемъ къ моему сочиненію «Неорганическая жизнь земли», Часть I. Идти назадъ.


Комментариев нет:
Отправить комментарий